题目内容
设偶函数f（x）的定义域为（﹣∞，0）∪（0，+∞），当x＞0时，f（x）=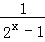 
．
（1）求当x＜0时，f（x）的解析式；
（2）求不等式 f（2x﹣3）＞1的解集．
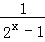．（1）求当x＜0时，f（x）的解析式；
（2）求不等式 f（2x﹣3）＞1的解集．
解：（1）当x＜0时，﹣x＞0，
∴f（﹣x）=
= 
又 f（x）是偶函数
∴f（x）=f（﹣x）=
（2）依题意，f（x）是偶函数，
当x＞0时，f（x）=
是减函数，且f（1）=1
由 f（2x﹣3）＞1可得 f（2x﹣3）＞f（1）
所以|2x﹣3|＜1，解得 1＜x＜2
不等式 的解集为 （1，2）
∴f（﹣x）=
= 又 f（x）是偶函数
∴f（x）=f（﹣x）=
（2）依题意，f（x）是偶函数，
当x＞0时，f（x）=
是减函数，且f（1）=1 由 f（2x﹣3）＞1可得 f（2x﹣3）＞f（1）
所以|2x﹣3|＜1，解得 1＜x＜2
不等式 的解集为 （1，2）
练习册系列答案
相关题目
，由定积分的几何意义和性质可知，
＝
设
f(x)是连续函数，且为偶函数，在对称区间[－a，a]上的积分
，由定积分的几何意义和性质得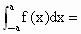
[
]|
A ．0 |
B ． |
|
C ． |
D ． |