题目内容
【题目】已知抛物线![]() 的方程
的方程![]() 为抛物线
为抛物线![]() 上一点,
上一点,![]() 为抛物线的焦点.
为抛物线的焦点.
(I)求![]() ;
;
(II)设直线![]() 与抛物线
与抛物线![]() 有唯一公共点
有唯一公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(I)![]() ;(II)存在,
;(II)存在,![]() .
.
【解析】
试题分析:(I)借助题设条件运用抛物线的定义求解;(II)借助题设运用直线与抛物线的位置关系及向量的数量积探求.
试题解析:
(I)由题可知![]() ,即
,即![]() ,由抛物线的定义可知
,由抛物线的定义可知![]() ............4分
............4分
(II)法1:由![]() 关于
关于![]() 轴对称可知,若存在点
轴对称可知,若存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则点
,则点![]() 必在
必在![]() 轴上,设
轴上,设![]() ,又设点
,又设点 ,由直线
,由直线![]() 与曲线
与曲线![]() 有唯一公共点
有唯一公共点![]() 知,直线
知,直线![]() 与
与![]() 相切由
相切由![]() 得
得![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得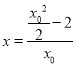 ,
,![]()
![]() 点坐标为
点坐标为![]() ,
,![]()
![]() ,
,![]()
![]() 点
点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,![]()
要使方程恒成立,必须有 ,解得
,解得![]() .
.
![]() 在坐标平面内存在点
在坐标平面内存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,其坐标为
,其坐标为![]() ..................12分
..................12分
法2:设点![]() ,由
,由![]() 与曲线
与曲线![]() 有唯一公共点
有唯一公共点![]() 知,直线
知,直线![]() 与
与![]() 相切,
相切,
由![]() 得
得![]() .
.![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() ,
,![]()
![]() 点坐标为
点坐标为![]() ,
,
![]() 以
以![]() 为直径的圆的方程为:
为直径的圆的方程为: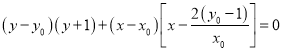 ①
①
分别令![]() 和
和![]() ,由点
,由点![]() 在曲线
在曲线![]() 上得
上得![]() ,
,
将![]() 的值分别代入①得:
的值分别代入①得:![]() ②
②
![]() ③
③
②③联立得![]() 或
或![]() .
.
![]() 在坐标平面内若存在点
在坐标平面内若存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则点
,则点![]() 必为
必为![]() 或
或![]() ,将
,将![]() 的坐标代入①式得,
的坐标代入①式得,
左边=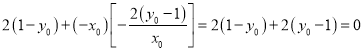 =右边,
=右边,
将![]() 的坐标代入①式得,左边=
的坐标代入①式得,左边=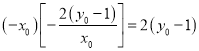 不恒等于0,
不恒等于0,
![]() 在坐标平面内若存在点
在坐标平面内若存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .........12分
.........12分

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: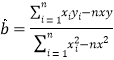 ,
,![]()