��Ŀ����
�����������⣺����f��x��=2x3+3�ķ�����Ϊf-1��x������f-1��5��=1��
�ڹ�ԭ����Բx2+y2-12x+9=0�������ߣ������������е��ӻ���Ϊ
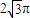 ��
�����ڡ�ABC�У���֪a=5��b=6��A=30°����B��һ����
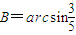 ��
����������Ƶ�ʷֲ�ֱ��ͼ�У��������������Σ��������С���ɵȲ�����{an}����a2+a3=0.8�������ij����ε����Ϊ
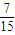
������ȷ��������Ϊ ��
���𰸡�����������ԭ�����뷴����֮��Ĺ�ϵ�õ�����ȷ�����ݻ���������õ��ڲ���ȷ�����������ν�ĸ������жϵõ��۲���ȷ������Ƶ�ʷֲ�ֱ��ͼ�õ�����ȷ��
����⣺��f��x��=2x3+3�ķ�����Ϊf-1��x������f-1��5��=1����1����ԭ�����õ�����ֵʱ5���ʢ���ȷ��
��ԭ����Բx2+y2-12x+9=0�������ߣ�
��Բ�������ߵĴ��ߣ�������ɵ�ֱ������������֮��Ĺ�ϵ���õ������������еĽ���60°��
����ԭ���ܳ����� ��������
��������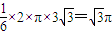 ���ʢڲ���ȷ��
���ʢڲ���ȷ��
�����������е��ӻ���Ϊ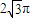 ��
��
�ڡ�ABC�У���֪a=5��b=6��A=30°��
��6��5��6×sin30°
��B�����⣬�ʢ۲���ȷ��
������Ƶ�ʷֲ�ֱ��ͼ�У��������������Σ��������С���ɵȲ�����{an}��
��a2+a3=0.8��a1=0.2��d=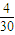 �������ij����ε����Ϊ0.2+
�������ij����ε����Ϊ0.2+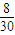 =
=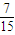 ���ʢ���ȷ��
���ʢ���ȷ��
���Ͽ�֪�٢���ȷ��
�ʴ�Ϊ���٢�
���������⿼���֪ʶ��Ƚ϶࣬�ر�ע����ڽ������εĿ���Ͷ��ڻ����Ŀ��飬�������Ĺؼ��Ƕ����������ĸ�������һ���жϣ�������һ���е���Ŀ��
����⣺��f��x��=2x3+3�ķ�����Ϊf-1��x������f-1��5��=1����1����ԭ�����õ�����ֵʱ5���ʢ���ȷ��
��ԭ����Բx2+y2-12x+9=0�������ߣ�
��Բ�������ߵĴ��ߣ�������ɵ�ֱ������������֮��Ĺ�ϵ���õ������������еĽ���60°��
����ԭ���ܳ�����
 ��������
��������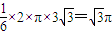 ���ʢڲ���ȷ��
���ʢڲ���ȷ�������������е��ӻ���Ϊ
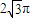 ��
���ڡ�ABC�У���֪a=5��b=6��A=30°��
��6��5��6×sin30°
��B�����⣬�ʢ۲���ȷ��
������Ƶ�ʷֲ�ֱ��ͼ�У��������������Σ��������С���ɵȲ�����{an}��
��a2+a3=0.8��a1=0.2��d=
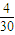 �������ij����ε����Ϊ0.2+
�������ij����ε����Ϊ0.2+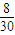 =
=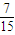 ���ʢ���ȷ��
���ʢ���ȷ�����Ͽ�֪�٢���ȷ��
�ʴ�Ϊ���٢�
���������⿼���֪ʶ��Ƚ϶࣬�ر�ע����ڽ������εĿ���Ͷ��ڻ����Ŀ��飬�������Ĺؼ��Ƕ����������ĸ�������һ���жϣ�������һ���е���Ŀ��

��ϰ��ϵ�д�
�����Ŀ
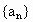 �ɵȱ����У�
�ɵȱ����У�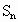 ��ǰn��ͣ���
��ǰn��ͣ���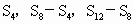 �ɵȱ����У�
�ɵȱ����У�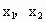 ����
����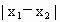 ����СֵΪ����������ֵΪ2������ֵΪ
����СֵΪ����������ֵΪ2������ֵΪ ��
��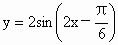 ��ͼ���һ���ԳƵ���
��ͼ���һ���ԳƵ��� ��
��