题目内容
已知函数![]()
![]()
(1)讨论![]() 的单调性与极值点。
的单调性与极值点。
(2)若![]() , 证明当
, 证明当![]() 时,
时,![]() 的图象恒在
的图象恒在![]() 的图象上方.
的图象上方.
解:(1)![]()
当![]() 时
时![]() 在(0,
在(0,![]() )上恒成立
)上恒成立
![]() 在(0,+∞)单调递增,此时
在(0,+∞)单调递增,此时![]() 无极值点
无极值点
当![]() 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
| x |
|
| ( |
|
| + | - | + |
|
| 增 | 减 | 增 |
由此表可知![]() 在(0 , 1)和(
在(0 , 1)和(![]() 上单调递增,
上单调递增, ![]() 在(1 ,
在(1 , ![]() )上单调递减
)上单调递减
![]() 为极大值点,
为极大值点,![]() 为极小值点 . ...............6分
为极小值点 . ...............6分
(2)![]() 时令
时令![]()
![]() 当
当![]() 时
时![]()
![]() 时,
时,![]()
![]() 在(0 1)递减,在(1,
在(0 1)递减,在(1,![]() 上递增.
上递增.
![]()
![]() 恒成立
恒成立
即![]() 时
时![]() 恒成立
恒成立
![]() 当
当![]()
![]() 的图象恒在
的图象恒在![]() 的图象的上方 ......12分
的图象的上方 ......12分

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
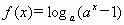 ,(
,(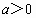 ,
,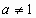 ),
),
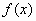 的定义域;
的定义域;
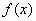 的单调性.
的单调性.