题目内容
在平面直角坐标系 中,已知直线
中,已知直线 的参数方程是
的参数方程是 (
( 为参数);以
为参数);以 为极点,
为极点, 轴正半轴为极轴的极坐标系中,圆
轴正半轴为极轴的极坐标系中,圆 的极坐标方程为
的极坐标方程为 .由直线
.由直线 上的点向圆
上的点向圆 引切线,求切线长的最小值.
引切线,求切线长的最小值.
 .
.
解析试题分析:先将圆 的极坐标方程化为直角坐标方程,再把直线上的点的坐标(含参数)代入,化为求函数的最值问题,也可将直线
的极坐标方程化为直角坐标方程,再把直线上的点的坐标(含参数)代入,化为求函数的最值问题,也可将直线 的参数方程化为普通方程,根据勾股定理转化为求圆心到直线上最小值的问题
的参数方程化为普通方程,根据勾股定理转化为求圆心到直线上最小值的问题
试题解析:因为圆 的极坐标方程为
的极坐标方程为 ,所以
,所以 ,
,
所以圆 的直角坐标方程为
的直角坐标方程为 ,圆心为
,圆心为 ,半径为1, 4分
,半径为1, 4分
因为直线 的参数方程为
的参数方程为 (
( 为参数),
为参数),
所以直线 上的点
上的点 向圆C 引切线长是
向圆C 引切线长是 ,
,
所以直线 上的点向圆C引的切线长的最小值是
上的点向圆C引的切线长的最小值是 . 10分
. 10分
考点:直线的参数方程和圆的极坐标方程,圆的切线长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )=
)= .
. ,直线l的极坐标方程为ρcos
,直线l的极坐标方程为ρcos =a,且点A在直线l上.
=a,且点A在直线l上. (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系. 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为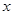 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程是
的参数方程是 (
( 是参数).若直线
是参数).若直线 的值.
的值. 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆 已知曲线
是圆心在极轴上,且经过极点的圆 已知曲线 对应的参数
对应的参数 ,射线
,射线 与曲线
与曲线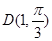
 ,
, 在曲线
在曲线 的值
的值  ,直线
,直线 的参数方程为
的参数方程为 ( t为参数,0≤
( t为参数,0≤ <
< ).
). 的参数方程为
的参数方程为 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为 .
. x +y的取值范围.
x +y的取值范围. )=6,圆C的参数方程为
)=6,圆C的参数方程为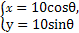 (θ为参数),求直线l被圆C截得的弦长.
(θ为参数),求直线l被圆C截得的弦长.