题目内容
若双曲线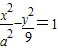 (a>0)的一条渐近线方程为3x-2y=0,则以双曲线的顶点和焦点分别为焦点和顶点的椭圆的离心率为 .
(a>0)的一条渐近线方程为3x-2y=0,则以双曲线的顶点和焦点分别为焦点和顶点的椭圆的离心率为 .
【答案】分析:根据给出的渐近线方程求出a=2,得出双曲线的顶点和焦点,也就是椭圆焦点和顶点,再求出离心率.
解答:解:双曲线 (a>0)的渐近线方程为3x±ay=0,由已知,a=2.
(a>0)的渐近线方程为3x±ay=0,由已知,a=2.
双曲线的顶点为(-2,0),(2,0)和焦点为(- ,0),(
,0),( ,0),
,0),
所以椭圆的顶点为(- ,0),(
,0),( ,0),焦点为(-2,0),(2,0),
,0),焦点为(-2,0),(2,0),
椭圆的离心率为e= =
= .
.
故答案为: .
.
点评:本题考查双曲线、椭圆的简单几何性质,属于基础题.难度不大,应准确熟练求解.
解答:解:双曲线
 (a>0)的渐近线方程为3x±ay=0,由已知,a=2.
(a>0)的渐近线方程为3x±ay=0,由已知,a=2.双曲线的顶点为(-2,0),(2,0)和焦点为(-
 ,0),(
,0),( ,0),
,0),所以椭圆的顶点为(-
 ,0),(
,0),( ,0),焦点为(-2,0),(2,0),
,0),焦点为(-2,0),(2,0),椭圆的离心率为e=
 =
= .
.故答案为:
 .
.点评:本题考查双曲线、椭圆的简单几何性质,属于基础题.难度不大,应准确熟练求解.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 (a>0)的一条渐近线方程为3x-2y=0,则a= .
(a>0)的一条渐近线方程为3x-2y=0,则a= . (a>0)的一条渐近线方程为3x-2y=0,则a= .
(a>0)的一条渐近线方程为3x-2y=0,则a= . (a>0)的一条渐近线方程为3x-2y=0,则a= .
(a>0)的一条渐近线方程为3x-2y=0,则a= . (a>0)的一条渐近线方程为3x-2y=0,则a= .
(a>0)的一条渐近线方程为3x-2y=0,则a= . (a>0)的一条渐近线方程为3x-2y=0,则a= .
(a>0)的一条渐近线方程为3x-2y=0,则a= .