题目内容
已知平面直角坐标系中,A(cosx,sinx),B(1,1), ,f(x)=|
,f(x)=| |2.
|2.(Ⅰ)求f(x)的最小正周期和对称中心;
(Ⅱ)求f(x)在区间[0,2π]上的单调递增区间.
【答案】分析:(I)利用数量积运算、两角和的正弦公式、三角函数的图象与性质即可得出.
(II)利用正弦函数的单调性即可得出.
解答:解:(Ⅰ)由题设知,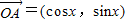 ,
,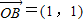 .
.
∴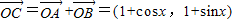 .
.
∴f(x)=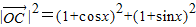
=2sinx+2cosx+3=2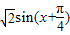
故最小正周期为2π.
对称中心横坐标满足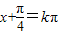 (k∈Z),即
(k∈Z),即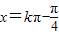 (k∈Z).
(k∈Z).
对称中心是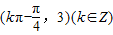 .
.
(Ⅱ)当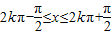 时f(x)单增,
时f(x)单增,
即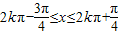 ,k∈Z.
,k∈Z.
又x∈[0,2π],故f(x)的递增区间为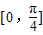 和
和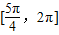 .
.
点评:熟练掌握数量积运算、两角和的正弦公式、三角函数的图象与性质是解题的关键.
(II)利用正弦函数的单调性即可得出.
解答:解:(Ⅰ)由题设知,
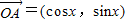 ,
,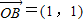 .
.∴
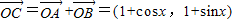 .
.∴f(x)=
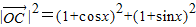
=2sinx+2cosx+3=2
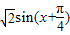
故最小正周期为2π.
对称中心横坐标满足
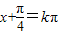 (k∈Z),即
(k∈Z),即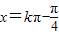 (k∈Z).
(k∈Z).对称中心是
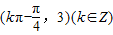 .
.(Ⅱ)当
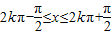 时f(x)单增,
时f(x)单增,即
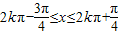 ,k∈Z.
,k∈Z.又x∈[0,2π],故f(x)的递增区间为
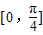 和
和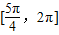 .
.点评:熟练掌握数量积运算、两角和的正弦公式、三角函数的图象与性质是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知平面直角坐标系中三点坐标分别为A(3,0),B(0,4),C(cosθ,sinθ),θ∈R,则△ABC面积的最大值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|