题目内容
数列{an}中,a1=1,an+1=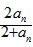 ,n∈N*,试猜想这个数列的通项公式。
,n∈N*,试猜想这个数列的通项公式。
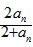 ,n∈N*,试猜想这个数列的通项公式。
,n∈N*,试猜想这个数列的通项公式。 解:在{an}中,a1=1,a2=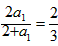 ,
,
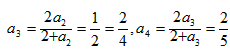 ,…
,…
∴{an}的通项公式为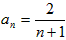
启示:
通过归纳推理得出的结论可能正确,也可能不正确,它的正确性需要经过严格的证明,本题的结论可用以下方法来证明,
∴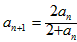 ,
,
∴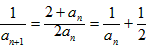 ,
,
∴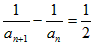
即数列{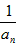 }是以
}是以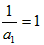 为首项,公差为
为首项,公差为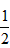 的等差数列,
的等差数列,
∴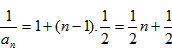 ,
,
∴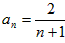 。
。

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
数列{an}中,a1=
,an+an+1=
,n∈N*,则
(a1+a2+…+an)等于( )
| 1 |
| 5 |
| 6 |
| 5n+1 |
| lim |
| n→∞ |
A、
| ||
B、
| ||
C、
| ||
D、
|