题目内容
(2012•通州区一模)已知椭圆C:
+
=1(a>b>0)的离心率为
,且短轴的一个端点到左焦点F的距离是
,经过点F且不垂直于x轴的直线l交椭圆C于A,B两点.点O为坐标原点.
(I)求椭圆C的标准方程;
(II)在线段OF上存在点M(m,0)(点M不与点O,F重合),使得以MA,MB为邻边的平行四边形MANB是菱形,求m的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 2 |
(I)求椭圆C的标准方程;
(II)在线段OF上存在点M(m,0)(点M不与点O,F重合),使得以MA,MB为邻边的平行四边形MANB是菱形,求m的取值范围.
分析:(Ⅰ)利用短轴的一个端点到左焦点点F的距离是
,离心率为
,可求椭圆几何量,从而可得椭圆C的标准方程;
(Ⅱ)设直线l的方程为y=k(x+1)(k≠0)代入椭圆方程,消去y可得一元二次方程,利用以MA,MB为邻边的平行四边形MANB是菱形,可得(
+
)•
=0,从而可得m=
,由此可得m的取值范围.
| 2 |
| ||
| 2 |
(Ⅱ)设直线l的方程为y=k(x+1)(k≠0)代入椭圆方程,消去y可得一元二次方程,利用以MA,MB为邻边的平行四边形MANB是菱形,可得(
| MA |
| MB |
| AB |
| -k2 |
| 1+2k2 |
解答:解:(Ⅰ)因为短轴的一个端点到左焦点点F的距离是
,离心率为
,
所以a=
,c=1
所以b2=a2-c2=1
所以椭圆C的标准方程是
+y2=1 …(4分)
(Ⅱ)因为直线l与x轴不垂直,且交椭圆C于A,B两点,所以设直线l的方程为y=k(x+1)(k≠0)
代入椭圆方程,消去y可得(1+2k2)x2+4k2x+2k2-2=0.
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
因为以MA,MB为邻边的平行四边形MANB是菱形,所以(
+
)•
=0.
所以(x1+x2-2m,y1+y2)•(x2-x1,y2-y1)=0
因为x1≠x2,
所以(x1+x2-2m)+k2(x2+x1+2)=0.
所以(
-2m)+k2(
+2)=0.
所以m=
.
因为k≠0,所以-
<m<0.
所以m的取值范围是-
<m<0.…(14分)
| 2 |
| ||
| 2 |
所以a=
| 2 |
所以b2=a2-c2=1
所以椭圆C的标准方程是
| x2 |
| 2 |
(Ⅱ)因为直线l与x轴不垂直,且交椭圆C于A,B两点,所以设直线l的方程为y=k(x+1)(k≠0)
代入椭圆方程,消去y可得(1+2k2)x2+4k2x+2k2-2=0.
设A(x1,y1),B(x2,y2),则x1+x2=
| -4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
因为以MA,MB为邻边的平行四边形MANB是菱形,所以(
| MA |
| MB |
| AB |
所以(x1+x2-2m,y1+y2)•(x2-x1,y2-y1)=0
因为x1≠x2,
所以(x1+x2-2m)+k2(x2+x1+2)=0.
所以(
| -4k2 |
| 1+2k2 |
| -4k2 |
| 1+2k2 |
所以m=
| -k2 |
| 1+2k2 |
因为k≠0,所以-
| 1 |
| 2 |
所以m的取值范围是-
| 1 |
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,正确运用韦达定理是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
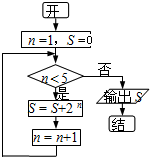 (2012•通州区一模)如图,程序框图所进行的求和运算是( )
(2012•通州区一模)如图,程序框图所进行的求和运算是( )