Question

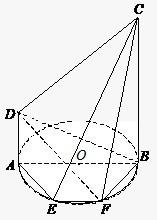如图，AB为圆O的直径，点E、F在圆上，已知AB∥EF，AB=BC=4，AE=EF=BF=2，AD=2．
直角梯形ABCD所在平面与圆O所在平面互相垂直．
（Ⅰ）求证：平面CBE⊥平面DAE；
（Ⅱ）求平面CDF与平面ABCD所成角的余弦值．

Answer 1

分析：（1）欲证平面CBE⊥平面DAE，根据面面垂直的判定定理可知在平面CBE内一直线与平面DAE垂直，
欲证BE⊥平面DAE，根据直线与平面垂直的判定定理可知只需证BE与平面DAE内两相交直线垂直，
AD⊥BE，AE⊥BE，AE∩AD=A，满足定理条件；
（2）连接OE，OF，以O为原点，OB所在的直线为y轴，垂直于OB的直线分别为x轴、z轴建立坐标系，
求出平面ABCD的一个法向量为

n1

以及平面CDF的一个法向量为

n2

，
求出两法向量的余弦值即可得到平面CDF与平面ABCD所成角的余弦值．

解答：解：（1）连接BE，因为四边形ABCD是直角梯形，
所以AD⊥AB，又平面ABCD⊥平面ABFE
所以AD⊥平面ABFE，所以AD⊥BE，
因为AB为O的直径，所以AE⊥BE，
又AE∩AD=A，所以BE⊥平面DAE，
又BE?平面CBE，所以平面CBE⊥平面DAE．
（2）如图，因为AE=EF=BF=2，连接OE，OF，
则△OEF是边长为2的等边三角形，以O为原点，
OB所在的直线为y轴，垂直于OB的直线分别为x轴、
z轴建立如如图所示的坐标系，则有
A（0，-2，0），B（0，2，0），C（0，2，4），
D（0，-2，2），F（

3

，1，0），
易得平面ABCD的一个法向量为

n1

=（1，0，0），
设平面CDF的一个法向量为

n2

=（x，y，z），
因为

CD

=（0，-4，-2），

CF

=（

3

，-1，-4），
则由

n1 • CD  =0 n2 • CF =0

可得

2y+z=0 3 x-y-4z=0

，令y=1，
得

n2

=（-

7

3

，1，-2），
所以cos＜

n1

，

n2

＞=-

7

8

．
结合图形，易知平面CDF与平面ABCD所成角的余弦值为

7

8

．

点评：本题主要考查了平面与平面垂直的判定，以及二面角的度量，空间向量是理科生需要掌握的，属于基础题．