题目内容
8. 在四边形ABCD中,∠DAB与∠DCB互补,AB=1,CD=DA=2,对角线BD=$\sqrt{7}$,
在四边形ABCD中,∠DAB与∠DCB互补,AB=1,CD=DA=2,对角线BD=$\sqrt{7}$,(1)求BC;
(2)求四边形ABCD的面积.
分析 (1)在△ADB中,△DCB中,分别使用余弦定理进行求解即可求BC;
(2)四边形ABCD的面积S=S△ADB+S△BDC.分别根据三角形的面积公式进行求解即可.
解答 解:(1)在△ADB中,cos∠DAB=$\frac{A{D}^{2}+A{B}^{2}-B{D}^{2}}{2AD•AB}$=$\frac{4+1-7}{2×2×1}=-\frac{1}{2}$,
即∠DAB=120°,则∠DCB=60°,
在△DCB中,cos∠DCB=$\frac{D{C}^{2}+B{C}^{2}-B{D}^{2}}{2DC•BC}=\frac{1}{2}$,
即$\frac{4+B{C}^{2}-7}{2×2BC}=\frac{1}{2}$,
即BC2-2BC-3=0.
解得BC=3或BC=-1(舍).
(2)四边形ABCD的面积S=S△ADB+S△BDC=$\frac{1}{2}AD•ABsin120°$+$\frac{1}{2}CD•BCsin60°$=$\frac{1}{2}×2×1×\frac{\sqrt{3}}{2}$+$\frac{1}{2}×2×3×\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
点评 本题主要考查解三角形的应用,根据余弦定理以及三角形的面积公式是解决本题的关键.

练习册系列答案
相关题目
16.据如图的流程图可得结果为( )
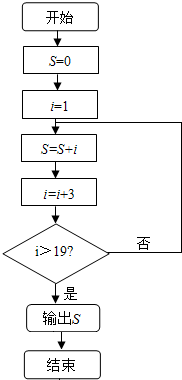

| A. | 19 | B. | 67 | C. | 51 | D. | 70 |
3.a,b,c为△ABC三边之长,若(a+b+c)(a+b-c)=ab,则△ABC的最大角为( )
| A. | 30° | B. | 120° | C. | 90° | D. | 60° |
18.在△ABC中,已知AC=$\sqrt{19}$,BC=2,B=$\frac{2π}{3}$,则边AC上的高为( )
| A. | $\frac{3\sqrt{19}}{19}$ | B. | $\frac{3\sqrt{57}}{19}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
 已知等差数列{an}中,a3=7,a6=16,将此等差数列的各项排成如下三角形数阵:则此数阵中第20行从左到右的第10个数是598.
已知等差数列{an}中,a3=7,a6=16,将此等差数列的各项排成如下三角形数阵:则此数阵中第20行从左到右的第10个数是598.