题目内容
对于函数f(x),若存在区间M=[a,b],(a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳定区间”现有四个函数:①f(x)=ex②f(x)=x3③
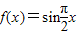 ④f(x)=lnx,其中存在“稳定区间”的函数有( )
④f(x)=lnx,其中存在“稳定区间”的函数有( )A.①②
B.②③
C.③④
D.②④
【答案】分析:根据“稳定区间”的定义,我们要想说明函数存在“稳定区间”,我们只要举出一个符合定义的区间M即可,但要说明函数没有“稳定区间”,我们可以用反证明法来说明.由此对四个函数逐一进行判断,即可得到答案.
解答:解:①对于函数f(x)=ex 若存在“稳定区间”[a,b],由于函数是定义域内的增函数,故有ea=a,eb=b,
即方程ex=x有两个解,即y=ex和y=x的图象有两个交点,这与即y=ex和y=x的图象没有公共点相矛盾,故①不存在“稳定区间”.
②对于f(x)=x3 存在“稳定区间”,如 x∈[0,1]时,f(x)=x3 ∈[0,1].
③对于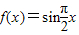 ,存在“稳定区间”,如 x∈[0,1]时,
,存在“稳定区间”,如 x∈[0,1]时,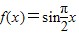 ∈[0,1].
∈[0,1].
④对于 f(x)=lnx,若存在“稳定区间”[a,b],由于函数是定义域内的增函数,故有lna=a,且lnb=b,即方程lnx=x 有两个解,
即y=lnx 和 y=x的图象有两个交点,这与y=lnx 和 y=x的图象没有公共点相矛盾,故④不存在“稳定区间”.
故选 B.
点评:本题考查的知识点是函数的概念及其构造要求,在说明一个函数没有“稳定区间”时,利用函数的性质、图象结合反证法证明是解答本题的关键.
解答:解:①对于函数f(x)=ex 若存在“稳定区间”[a,b],由于函数是定义域内的增函数,故有ea=a,eb=b,
即方程ex=x有两个解,即y=ex和y=x的图象有两个交点,这与即y=ex和y=x的图象没有公共点相矛盾,故①不存在“稳定区间”.
②对于f(x)=x3 存在“稳定区间”,如 x∈[0,1]时,f(x)=x3 ∈[0,1].
③对于
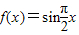 ,存在“稳定区间”,如 x∈[0,1]时,
,存在“稳定区间”,如 x∈[0,1]时,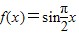 ∈[0,1].
∈[0,1].④对于 f(x)=lnx,若存在“稳定区间”[a,b],由于函数是定义域内的增函数,故有lna=a,且lnb=b,即方程lnx=x 有两个解,
即y=lnx 和 y=x的图象有两个交点,这与y=lnx 和 y=x的图象没有公共点相矛盾,故④不存在“稳定区间”.
故选 B.
点评:本题考查的知识点是函数的概念及其构造要求,在说明一个函数没有“稳定区间”时,利用函数的性质、图象结合反证法证明是解答本题的关键.

练习册系列答案
相关题目