Question

求通过直线l:2x+y+4=0及圆C:x²+y²+2x-4y+1=0的交点，并且有最小面积的圆的方程.

Answer 1

解析：解法一:圆的方程为(x+1)²+(y-2)²=4.设直线l与圆C交于A、B两点，D为AB的中点，则直线CD的方程为x-2y+5=0,x-2y+5=0,2x+y+4=0.故D

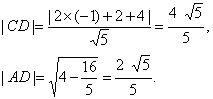
∴以D为圆心，AB为直径的圆是面积最小的圆.?

解法二:设圆的方程是(x²+y²+2x-4y+1)+λ(2x+y+4)=0,即［x+(1+λ)²］+

圆面积=πR²,?

而时，圆面积最小，此时圆的方程是5x²+5y²+26x-12y+37=0.?

解法三:设A(x₁,y₁),B(x₂,y₂),则以AB为直径的圆方程可设为(x-x₁)(x-x₂)+(y-y₁)(y-y₂)=0,?

即x²+y²-(x₁+x₂)x-(y₁+y₂)y+x₁x₂+y₁y₂=0.然后用韦达定理求出圆的方程.