题目内容
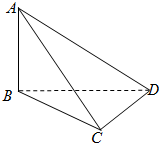 在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,且AB=3,BD=4,则三棱锥A-BCD外接球的半径为( )
在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,且AB=3,BD=4,则三棱锥A-BCD外接球的半径为( )| A、2 | ||
| B、3 | ||
| C、4 | ||
D、
|
分析:取AD的中点O,连结OB、OC.由线面垂直的判定与性质,证出AB⊥BD且AC⊥CD,得到△ABD与△ACD是具有公共斜边的直角三角形,从而得出OA=OB=OC=OD=
AD,所以A、B、C、D四点在以O为球心的球面上,再根据题中的数据利用勾股定理算出AD长,即可得到三棱锥A-BCD外接球的半径大小.
| 1 |
| 2 |
解答: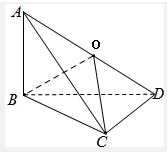 解:取AD的中点O,连结OB、OC
解:取AD的中点O,连结OB、OC
∵AB⊥平面BCD,CD?平面BCD,∴AB⊥CD,
又∵BC⊥CD,AB∩BC=B,∴CD⊥平面ABC,
∵AC?平面ABC,∴CD⊥AC,
∵OC是Rt△ADC的斜边上的中线,OC=
AD.
同理可得:Rt△ABD中,OB=
AD,
∴OA=OB=OC=OD=
AD,可得A、B、C、D四点在以O为球心的球面上.
Rt△ABD中,AB=3且BD=4,可得AD=
=5,
由此可得球O的半径R=
AD=
,即三棱锥A-BCD外接球的半径为
.
故选:D
 解:取AD的中点O,连结OB、OC
解:取AD的中点O,连结OB、OC∵AB⊥平面BCD,CD?平面BCD,∴AB⊥CD,
又∵BC⊥CD,AB∩BC=B,∴CD⊥平面ABC,
∵AC?平面ABC,∴CD⊥AC,
∵OC是Rt△ADC的斜边上的中线,OC=
| 1 |
| 2 |
同理可得:Rt△ABD中,OB=
| 1 |
| 2 |
∴OA=OB=OC=OD=
| 1 |
| 2 |
Rt△ABD中,AB=3且BD=4,可得AD=
| AB2+BD2 |
由此可得球O的半径R=
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
故选:D
点评:本题已知三棱锥的底面为直角三角形,由它的外接球的半径.着重考查了线面垂直的判定与性质、勾股定理与球内接多面体等知识,属于中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( )
如图,在三棱锥A-BCD中,DA,DB,DC两两垂直,且长度均为1,E为BC中点,则下列结论正确的是( ) 在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN=
在三棱锥A-BCD中,AB=4,CD=2,且异面直线AB、CD所成的角为60°,若M、N分别是AD、BC的中点,则MN= (2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD.
(2011•渭南三模)在三棱锥A-BCD中,BD=BC=1,BD⊥BC,DE⊥AB,AD=2,AD⊥平面BCD. 如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜
如图所示,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜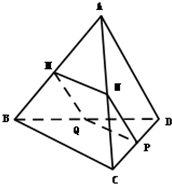 如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.
如图,在三棱锥A-BCD中,平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点,且MN=PQ.