题目内容
2.已知α,β为锐角,cosα=$\frac{1}{7},cos(α+β)=-\frac{11}{14}$,求cosβ的值及β的大小.分析 由题意和同角三角函数基本关系可得sinα和sin(α+β),代入cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα,计算可得.
解答 解:∵α,β为锐角,cosα=$\frac{1}{7},cos(α+β)=-\frac{11}{14}$,
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{4\sqrt{3}}{7}$,同理sin(α+β)=$\frac{5\sqrt{3}}{14}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα
=$-\frac{11}{14}$×$\frac{1}{7}$+$\frac{4\sqrt{3}}{7}$×$\frac{5\sqrt{3}}{14}$=$\frac{1}{2}$,∴β=$\frac{π}{3}$
点评 本题考查两角和与差的余弦公式,涉及同角三角函数基本关系,属基础题.

练习册系列答案
相关题目
7.下列四组函数中,表示相同函数的一组是( )
| A. | f(x)=1,g(x)=$\frac{x}{x}$ | B. | f(x)=$\sqrt{x+1}$•$\sqrt{x-1}$,g(x)=$\sqrt{{x}^{2}-1}$ | ||
| C. | f(x)=x,g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 |
14.计算$\frac{2i}{1-i}$(i为虚数单位)等于( )
| A. | 1-i | B. | -1-i | C. | -1+i | D. | 1+i |
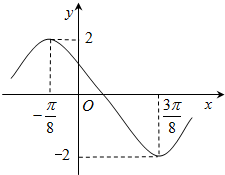 已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.