题目内容
8.已知定义在x∈[-2,2]上的偶函数f(x)满足:当x∈[0,2]时,f(x)=-x+2$\sqrt{3-x}$.(1)求函数f(x)在x∈[-2,2]上的解析式;
(2)设g(x)=ax-2-a,(a>0),若对于任意x1,x2∈[-2,2],都有g(x1)<f(x2)成立,求实数a的取值范围.
分析 (1)设x∈[-2,0],则-x∈[0,2],结合函数的奇偶性,从而求出函数的解析式;
(2)由题意得g(x)max<f(x)min,分别求出g(x)的最大值和f(x)的最小值,得到关于a的不等式,从而求出a的范围.
解答 解:(1)设x∈[-2,0],则-x∈[0,2],
∵f(x)定义x∈[-2,2]是偶函数,
∴f(-x)=x+2$\sqrt{3+x}$,
∵f(-x)=f(x),∴f(x)=x+2$\sqrt{3+x}$,
∴f(x)=$\left\{\begin{array}{l}{x+2\sqrt{3+x},x∈[-2,0)}\\{-x+2\sqrt{3-x},x∈[0,2]}\end{array}\right.$;
(2)因为对任意x1,x2∈[-2.,2],都有g(x1)<f(x2)成立,
所以g(x)max<f(x)min,
又因为f(x)是定义在[-2,2]上的偶函数,
∴f(x)在区间[-2,0]和区间[0,2]上的值域相同.
当x∈[-2,0]时:f(x)=x+2$\sqrt{3+x}$,
设t=$\sqrt{3+x}$,则t∈[1,$\sqrt{3}$],
函数化为:y=t2+t-3,t∈[1,$\sqrt{3}$],
则f(x)min=-1,
又g(x)max=g(2)=a-2,
∴a-2<-1,∴a<1,
故a的范围是:0<a<1.
点评 本题考查了求函数的解析式问题,考查函数的奇偶性、函数恒成立问题,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.计算$\frac{5}{i-2}$(i为虚数单位)的值是( )
| A. | i+2 | B. | i-2 | C. | -2-i | D. | 2-i |
16.下表是关于出生男婴与女婴调查的列联表:
那么A=47,B=82.
| 晚上 | 白天 | 总计 | |
| 男婴 | 45 | A | 92 |
| 女婴 | 53 | 35 | 88 |
| 总计 | 98 | B | 180 |
20.已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x>1),则最大角为( )
| A. | 150° | B. | 120° | C. | 60° | D. | 75° |
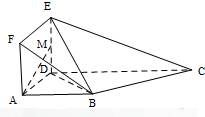 如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.
如图所示,已知多面体ABCDEF,平面ADEF⊥平面ABCD,ADEF为正方形,ABCD为直角梯形,且AB∥CD,AB⊥AD,AB=AD=$\frac{1}{2}$CD=1,M为线段ED上的动点.