题目内容
已知函数f（x）=lg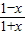
，若f（a）=b，则f（-a）等于（ ）A．b
B．-b
C．
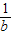
D．-
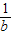
【答案】分析：方法一：将-a代入函数解析式变形整理即可
访求二：用定义可以验证f（-x）=-f（x），故函数f（x）是奇函数，利用奇函数的性质求解．
解答：解：方法一：f（-a）=lg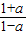
=-lg
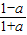=-f（a）=-b．
方法二：f（-x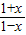）=lg
=-lg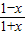
=-f（x），
故函数f（x）是奇函数，
∵f（a）=b，∴f（-a）=-b
故应选 B．
点评：考查奇函数的定义法证明（方法二）及利用定义法证明中的变形技巧（方法一）做题．
访求二：用定义可以验证f（-x）=-f（x），故函数f（x）是奇函数，利用奇函数的性质求解．
解答：解：方法一：f（-a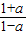）=lg
=-lg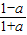=-f（a）=-b．方法二：f（-x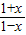）=lg
=-lg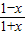=-f（x），故函数f（x）是奇函数，
∵f（a）=b，∴f（-a）=-b
故应选 B．
点评：考查奇函数的定义法证明（方法二）及利用定义法证明中的变形技巧（方法一）做题．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目