题目内容
在数列{ an }中，a1=1，an+1=3an（n∈N*），则a4等于（ ）
| A、9 | B、10 | C、27 | D、81 |
分析：利用等比数列的通项公式即可得出．
解答：解：∵在数列{ an }中，a1=1，an+1=3an（n∈N*），
∴数列{ an }是等比数列，公比为3．
∴an=a1qn-1=3n-1．
∴a4=33=27．
故选：C．
∴数列{ an }是等比数列，公比为3．
∴an=a1qn-1=3n-1．
∴a4=33=27．
故选：C．
点评：本题考查了等比数列的通项公式，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在数列（an）中，an=2n-7，则当前n项和取得最小值时的n的等于（ ）
| A、3 | B、4 | C、3或4 | D、4或5 |
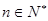),则该数列的通项an= 。