题目内容
若函数
的最大值为
，则函数
的图象的一条对称轴方程为
A． | B． | C． | D． |
B
解析试题分析：由函数可化为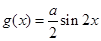
.又因为函数
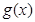的最大值为.所以
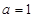.所以函数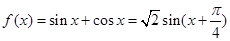
.正弦函数的对称轴即函数值为最大或最小时x的值，通过将下列四个选项逐一代入可知成立.故选B.
考点：1.三角函数的最值.2.二倍角公式.3.化一公式.4.三角函数的对称轴.
练习册系列答案
名校课堂系列答案
相关题目
函数
的部分图象如图所示，则
的值分别是（ ）
A． | B． | C． | D． |
若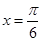
是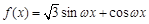
的图象的一条对称轴，则
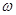可以是（ ）
| A．4 | B．8 | C．2 | D．1 |
函数y=sin2x+sinx-1的值域为( )
| A．[-1,1] | B．[- ,-1] |
| C．[-,1] | D．[-1,] |
已知a∈R，sin α＋2cos α＝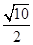
，则tan 2α＝( )
A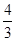． | B． | C．－ | D．－ |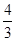
给定命题p：函数y＝sin
和函数y＝cos
的图象关于原点对称；命题q：当x＝kπ＋
(k∈Z)时，函数y＝
(sin 2x＋cos 2x)取得极小值．下列说法正确的是( )
| A．p∨q是假命题 | B．¬p∧q是假命题 |
| C．p∧q是真命题 | D．¬p∨q是真命题 |
已知α为锐角，cos α＝
，则tan
＝( )
| A．－3 | B．－ |
C．－ | D．－7 |
已知函数f(x)=3cos(2x-
)在[0,
]上的最大值为M,最小值为m,则M+m等于( )
| A．0 | B．3+ |
| C．3- | D． |
函数f(x)＝sin x－cos
的值域为( )
| A．[－2，2] | B．[－ ，] | C．[－1，1] | D． |