题目内容
直线y=kx+b与曲线x2+4y2-4=0交于A、B两点,记△AOB的面积为S(O是坐标原点).(1)求曲线的离心率;
(2)求在k=0,0<b<1的条件下,S的最大值.
【答案】分析:(1)将方程化为标准方程,求得几何量,即可求得离心率;
(2)求出A,B的坐标,可得△AOB的面积,利用基本不等式,即可求得结论.
解答: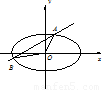 解:(1)曲线的方程可化为:
解:(1)曲线的方程可化为: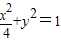 ,-------------------(1分)
,-------------------(1分)
∴此曲线为椭圆,a=2,c=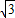 -------------------(4分)
-------------------(4分)
∴此椭圆的离心率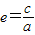
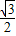 ------------------(6分)
------------------(6分)
(2)设点A的坐标为(x1,b),点B的坐标为(x2,b),
由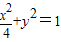 及y=b,解得x1,2=±2
及y=b,解得x1,2=±2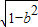 ,-----------------------------(8分)
,-----------------------------(8分)
所以S= b|x1-x2|=2b
b|x1-x2|=2b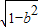 ≤b2+1-b2=1-----------------------------(11分)
≤b2+1-b2=1-----------------------------(11分)
当且仅当b=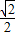 时,S取到最大值1.-----------------------------(13分)
时,S取到最大值1.-----------------------------(13分)
点评:本题考查椭圆的几何性质,考查三角形面积的计算,考查基本不等式的运用,属于基础题.
(2)求出A,B的坐标,可得△AOB的面积,利用基本不等式,即可求得结论.
解答:
 解:(1)曲线的方程可化为:
解:(1)曲线的方程可化为: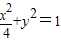 ,-------------------(1分)
,-------------------(1分)∴此曲线为椭圆,a=2,c=
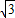 -------------------(4分)
-------------------(4分)∴此椭圆的离心率
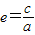
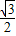 ------------------(6分)
------------------(6分)(2)设点A的坐标为(x1,b),点B的坐标为(x2,b),
由
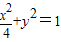 及y=b,解得x1,2=±2
及y=b,解得x1,2=±2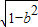 ,-----------------------------(8分)
,-----------------------------(8分)所以S=
 b|x1-x2|=2b
b|x1-x2|=2b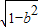 ≤b2+1-b2=1-----------------------------(11分)
≤b2+1-b2=1-----------------------------(11分)当且仅当b=
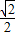 时,S取到最大值1.-----------------------------(13分)
时,S取到最大值1.-----------------------------(13分)点评:本题考查椭圆的几何性质,考查三角形面积的计算,考查基本不等式的运用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
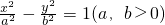 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y=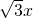 ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且 .
. 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y= ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且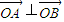 .
.