题目内容

已知数列{an}是等差数列,其前n项和为Sn,a3=7,S4=24.

(1)求数列{an}的通项公式;

(2)设p,q是正整数,且p≠q,求证:Sp+q＜(S2p+S2q).

(1)解:设等差数列{an}的公差是d,依题意,得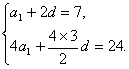解得a1=3,d=2.

∴数列{an}的通项公式为an=a1+(n-1)d=2n+1.

(2)证明:∵an=2n+1,

∴Sn==n2+2n.

∵2Sp+q-(S2p+S2q)=2［(p+q)2+2(p+q)］-(4p2+4p)-(4q2+4q)=-2(p-q)2,

而p≠q,故2Sp+q-(S2p+S2q)＜0.

∴Sp+q＜(S2p+S2q).

练习册系列答案
相关题目
定义一个“等积数列”：在一个数列中，如果每一项与它后一项的积都是同一常数，那么这个数列叫“等积数列”，这个常数叫做这个数列的公积．已知数列{an}是等积数列，且a1=2，公积为5，则这个数列的前n项和Sn的计算公式为：
 
．
在一个数列中，如果?n∈N*，都有an•an+1•an+2=k（k为常数），那么这个数列叫做等积数列，k叫做这个数列的公积．已知数列{an}是等积数列，且a1=1，a2=3，公积为27，则a1+a2+a3+…+a18=
78
78
．
定义“等积数列”：在一个数列中，如果每一个项与它的后一项的积都为同一个常数，那末这个数列叫做等积数列，这个常数叫做该数列的公积．已知数列{an}是等积数列，且a1=2，公积为5，Tn为数列{an}前n项的积，则T2011=
51006
2
51006
2
．
我们对数列作如下定义，如果?n∈N*，都有anan+1an+2=k（k为常数），那么这个数列叫做等积数列，k叫做这个数列的公积．已知数列{an}是等积数列，且a1=1，a2=2，公积为6，则a1+a2+a3+…+a9=
18
18
．
已知等差数列的定义为：在一个数列中，从第二项起，如果每一项与它的前一项的差都为同一个常数，那么这个数列叫做等差数列，这个常数叫做该数列的公差．
（1）类比等差数列的定义给出“等和数列”的定义；
（2）已知数列{an}是等和数列，且a1=2，公和为5，求 a18的值，并猜出这个数列的通项公式（不要求证明）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网