题目内容
已知函数
在区间[1，2]内单调递减，则实数a的取值范围是
- A.
- B.a≥9
- C.a≤3
- D.
B
分析：由函数在区间[1，2]内单调递减，转化成f'（x）≤0在[1，2]内恒成立，利用参数分离法即可求出a的范围．
解答：∵函数在区间[1，2]内单调递减，，
∴f'（x）=3x2-ax+6≤0在[1，2]内恒成立．
即 a≥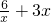
在[1，2]内恒成立．
∵t=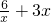 在[1，2]上的最大值为9，
∴a≥9．
故选B．
点评：此题主要考查利用导函数的正负判断原函数的单调性，关于不等式恒成立问题要转化成求最值问题来解决，属于基础题．
分析：由函数
在区间[1，2]内单调递减，转化成f'（x）≤0在[1，2]内恒成立，利用参数分离法即可求出a的范围．解答：∵函数
在区间[1，2]内单调递减，，∴f'（x）=3x2-ax+6≤0在[1，2]内恒成立．
即 a≥
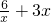在[1，2]内恒成立．∵t=
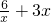在[1，2]上的最大值为9，∴a≥9．
故选B．
点评：此题主要考查利用导函数的正负判断原函数的单调性，关于不等式恒成立问题要转化成求最值问题来解决，属于基础题．
练习册系列答案
步步高达标卷系列答案
相关题目
在区间[1，2]上是增函数，且
在区间[0，1]上是减函数。
的值；
图象上任意一点，求点P到直线
距离的最小值；
且
时，
恒成立，求
的取值范围。
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为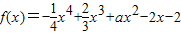 
在区间[-1，1]上单调递减，在区间[1，2]上单调递增，
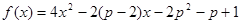在区间[-1，1]上至少存在一个实数c使f（c）>0，则实数p的范围 ．
在区间[1,2]上不是单调函数,则错误!不能通过编辑域代码创建对象。的范围为