题目内容
【题目】已知f（x）=ln（ax+b）+x2（a≠0）．
（1）若曲线y=f（x）在点（1，f（1））处的切线方程为y=x，求a，b的值；
（2）若f（x）≤x2+x恒成立，求ab的最大值．
【答案】
（1）解：∵f（x）=ln（ax+b）+x2（a≠0），
∴ 
，
∵曲线y=f（x）在点（1，f（1））处的切线方程为y=x，
∴ 
，
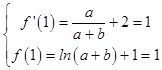解得，a=﹣1，b=2；
（2）解：设g（x）=f（x）﹣（x2+x），则g（x）=ln（ax+b）﹣x，依题意g（x）≤0恒成立，
①a＜0时，g（x）定义域 
，
取x0使得 
，得 
，
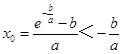则 
与g（x）≤0矛盾，∴a＜0不符合要求，
②a＞0时，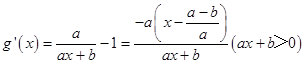 
，
当 
时，g'（x）＞0；当 
时，g'（x）＜0，
∴g（x）在区间 
上为增函数，在区间 
上为减函数，
∴g（x）在其定义域 
上有最大值，最大值为 
，
由g（x）≤0，得 
，∴b≤a﹣alna，∴ab≤a2﹣a2lna，
设h（a）=a2﹣a2lna，则h'（a）=2a﹣（2alna+a）=a（1﹣2lna），
∴ 
时， 
时，h'（a）＜0，
∴h（a）在区间 
上为增函数，在区间 
上为减函数，
∴h（a）的最大值为 
，
∴当 
时，ab取最大值为 
，
综合①，②得，ab最大值为 ．
【解析】（1）推导出 
，利用导数的几何意义列出方程组，能求出a，b的值．（2）设g（x）=f（x）﹣（x2+x），则g（x）=ln（ax+b）﹣x，依题意g（x）≤0恒成立，根a＜0，a＞0两种情况分类讨论，利用导数性质能求出ab的最大值．
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点，需要掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值才能正确解答此题．
