题目内容
某班运动队由足球运动员18人、篮球运动员12人、乒乓球运动员6人组成,现从这些运动员中抽取1个容量为n的样本,若分别采用系统抽样和分层抽样,则都不用剔除个体;当样本容量为n+1个时,若采用系统抽样,则需要剔除1个个体,那么样本容量n为
- A.5
- B.6
- C.12
- D.18
B
分析:由题意知采用系统抽样和分层抽样方法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,算出总体个数,根据分层抽样的比例和抽取的乒乓球运动员人数得到n应是6的倍数,36的约数,由系统抽样得到 必须是整数,验证出n的值.
必须是整数,验证出n的值.
解答:由题意知采用系统抽样和分层抽样方法抽取,不用剔除个体;
如果样本容量增加一个,则在采用系统抽样时,
需要在总体中先剔除1个个体,
∵总体容量为6+12+18=36.
当样本容量是n时,由题意知,系统抽样的间隔为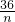 ,
,
分层抽样的比例是 ,抽取的乒乓球运动员人数为
,抽取的乒乓球运动员人数为 •6=
•6= ,
,
篮球运动员人数为 •12=
•12=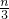 ,足球运动员人数为
,足球运动员人数为 •18=
•18= ,
,
∵n应是6的倍数,36的约数,
即n=6,12,18.
当样本容量为(n+1)时,总体容量是35人,
系统抽样的间隔为 ,
,
∵ 必须是整数,
必须是整数,
∴n只能取6.
即样本容量n=6.
故选B.
点评:本题考查分层抽样和系统抽样,是一个用来认识这两种抽样的一个题目,把两种抽样放在一个题目中考查,加以区分,是一个好题.
分析:由题意知采用系统抽样和分层抽样方法抽取,不用剔除个体;如果样本容量增加一个,则在采用系统抽样时,需要在总体中先剔除1个个体,算出总体个数,根据分层抽样的比例和抽取的乒乓球运动员人数得到n应是6的倍数,36的约数,由系统抽样得到
 必须是整数,验证出n的值.
必须是整数,验证出n的值.解答:由题意知采用系统抽样和分层抽样方法抽取,不用剔除个体;
如果样本容量增加一个,则在采用系统抽样时,
需要在总体中先剔除1个个体,
∵总体容量为6+12+18=36.
当样本容量是n时,由题意知,系统抽样的间隔为
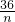 ,
,分层抽样的比例是
 ,抽取的乒乓球运动员人数为
,抽取的乒乓球运动员人数为 •6=
•6= ,
,篮球运动员人数为
 •12=
•12=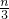 ,足球运动员人数为
,足球运动员人数为 •18=
•18= ,
,∵n应是6的倍数,36的约数,
即n=6,12,18.
当样本容量为(n+1)时,总体容量是35人,
系统抽样的间隔为
 ,
,∵
 必须是整数,
必须是整数,∴n只能取6.
即样本容量n=6.
故选B.
点评:本题考查分层抽样和系统抽样,是一个用来认识这两种抽样的一个题目,把两种抽样放在一个题目中考查,加以区分,是一个好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目