题目内容
已知正项数列{an}的前n项和为Sn,且满足Sn+an=1,
(1)求数列{an} 的通项公式;
(2)设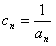 ,则是否存在数列{bn},满足b1c1+b2c2+…+bncn=(2n-1)2n+1+2对一切正整数n都成立?若存在,请求出数列{bn}的通项公式;若不存在,请说明理由。
,则是否存在数列{bn},满足b1c1+b2c2+…+bncn=(2n-1)2n+1+2对一切正整数n都成立?若存在,请求出数列{bn}的通项公式;若不存在,请说明理由。
(1)求数列{an} 的通项公式;
(2)设
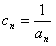 ,则是否存在数列{bn},满足b1c1+b2c2+…+bncn=(2n-1)2n+1+2对一切正整数n都成立?若存在,请求出数列{bn}的通项公式;若不存在,请说明理由。
,则是否存在数列{bn},满足b1c1+b2c2+…+bncn=(2n-1)2n+1+2对一切正整数n都成立?若存在,请求出数列{bn}的通项公式;若不存在,请说明理由。解:(1)当n=1时, ,故
,故 ;
;
当 时,
时, ,
,
两式相减得到 ,
,
所以数列 为首项为
为首项为 ,公比为
,公比为 的等比数列,
的等比数列,
所以 。
。
(2)因为 ,
,
所以 ,
,
若存在满足题意的数列 ,
,
则 ,
,
两式相减,得到 ,
,
由 ,
,
得到 ,满足上式。
,满足上式。
所以,存在满足题意的数列 ,通项公式为
,通项公式为 。
。
 ,故
,故 ;
;当
 时,
时, ,
,两式相减得到
 ,
,所以数列
 为首项为
为首项为 ,公比为
,公比为 的等比数列,
的等比数列,所以
 。
。 (2)因为
 ,
,所以
 ,
,若存在满足题意的数列
 ,
,则
 ,
,两式相减,得到
 ,
,由
 ,
,得到
 ,满足上式。
,满足上式。所以,存在满足题意的数列
 ,通项公式为
,通项公式为 。
。
练习册系列答案
相关题目