题目内容
数列1，1＋2，1＋2＋4，…，1＋2＋22＋…＋2n－1，…的前n项和Sn>1020，那么n的最小值是（ ）
| A．7 | B．8 | C．9 | D．10 |
D
解析试题分析：依题意，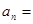
1+2+22+…+2n-1=
=2n-1，
∴Sn=（21-1）+（22-1）+…+（2n-1）
=（21+22+…+2n）-n
=
=2n+1-n-2．
因为Sn>1020，即2n+1-n-2>1020，代答案可得
考点：数列的求和，突出考查等比数列的求和公式．
练习册系列答案
相关题目
已知向量
，且
，则实数
=（ ）
A． | B．0 | C．3 | D． |
已知递减的等差数列
满足
，则数列的前
项和
取最大值时，
=（ ）
| A．3 | B．4或5 | C．4 | D．5或6 |
设
是各项为正数的等比数列，
是其公比，
是其前
项的积，且
，则下列结论错误的是（ ）
A． | B． |
C． | D． 与 均为的最大值 |
已知数列{a
}的前n项和
满足：
，且
=1．那么
=（ ）
| A．1 | B．9 | C．10 | D．55 |
。下列四个命题
其中的真命题是（ ）
A． ， | B．, | C． , | D．, |
设
是定义在R上的偶函数，且在
上是增函数，
，
，
，则
的大小关系是（ ）
A． | B． |
C． | D． |
， 
，
，则球的表面积为( )
B.
C. 
D. 