题目内容
已知向量
(1)若 ⊥(
⊥(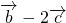 ),求tan(α+β)的值;
),求tan(α+β)的值;
(2)若 ∥
∥ ,求tanαtanβ的值.
,求tanαtanβ的值.
解:(1)由题意可得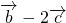 =(sinβ-2cosβ,4cosβ+8sinβ),
=(sinβ-2cosβ,4cosβ+8sinβ),
∵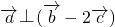 ,∴
,∴ ,
,
即4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,
化简得:4cosαsinβ+4sinαcosβ-8cosαcosβ+8sinαsinβ=0,
即4sin(α+β)=8cos(α+β),
∴tan(α+β)= =2;
=2;
(2)由 ∥
∥ 可得4cosα×4cosβ-sinαsinβ=0,
可得4cosα×4cosβ-sinαsinβ=0,
即tanαtanβ= =16
=16
分析:(1)由题意可得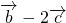 =(sinβ-2cosβ,4cosβ+8sinβ),进而可得4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,由三角函数的定义即可得结果;(2)由向量平行的充要条件
=(sinβ-2cosβ,4cosβ+8sinβ),进而可得4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,由三角函数的定义即可得结果;(2)由向量平行的充要条件
可得4cosα×4cosβ-sinαsinβ=0,由三角函数的公式可得tanαtanβ= ,化简即可.
,化简即可.
点评:本题考查三角函数的运算和向量的平行与垂直,记准公式是解决问题的关键,属中档题.
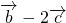 =(sinβ-2cosβ,4cosβ+8sinβ),
=(sinβ-2cosβ,4cosβ+8sinβ),∵
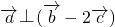 ,∴
,∴ ,
,即4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,
化简得:4cosαsinβ+4sinαcosβ-8cosαcosβ+8sinαsinβ=0,
即4sin(α+β)=8cos(α+β),
∴tan(α+β)=
 =2;
=2;(2)由
 ∥
∥ 可得4cosα×4cosβ-sinαsinβ=0,
可得4cosα×4cosβ-sinαsinβ=0,即tanαtanβ=
 =16
=16分析:(1)由题意可得
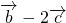 =(sinβ-2cosβ,4cosβ+8sinβ),进而可得4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,由三角函数的定义即可得结果;(2)由向量平行的充要条件
=(sinβ-2cosβ,4cosβ+8sinβ),进而可得4cosα(sinβ-2cosβ)+sinα(4cosβ+8sinβ)=0,由三角函数的定义即可得结果;(2)由向量平行的充要条件可得4cosα×4cosβ-sinαsinβ=0,由三角函数的公式可得tanαtanβ=
 ,化简即可.
,化简即可.点评:本题考查三角函数的运算和向量的平行与垂直,记准公式是解决问题的关键,属中档题.

练习册系列答案
相关题目

 ,求实数m的值。
,求实数m的值。 ,求△ABC面积的最大值.
,求△ABC面积的最大值.

 ,求
,求 的值;
的值; ,
, 在
在 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是 ,且满
,且满 ,求
,求 的取值范围。
的取值范围。

 ,求
,求 的值;
的值; ,
, 与
与 所成的角为
所成的角为 ,求
,求