题目内容
△ABC中，角A、B、C的对边分别为a，b，c．
（Ⅰ）若
，求cosA的值；
（Ⅱ）若A∈[
，
]，求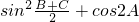
的取值范围．
解：（Ⅰ）∵，
∴
．∴
．
（Ⅱ）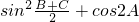
=
=
=2cos2A+
cosA-
=2（cosA+
）2-
，
∵A∈[，]，
∴cosA∈[-，0]．
∴2（cosA+）2-∈[-，-
]．
即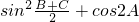的取值范围是[-，-]．
分析：（1）欲求cosA根据条件，借助余弦定理即得
（2）利用降幂公式和二倍角公式化简成关于cosA的二次函数进行求解
点评：本题综合考查了余弦定理，二次函数的最值问题，通过换元法转化成二次函数进行求解．
，∴
．∴．（Ⅱ）
=
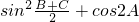
==2cos2A+
cosA-=2（cosA+
）2-，∵A∈[
，]，∴cosA∈[-
，0]．∴2（cosA+
）2-∈[-，-]．即
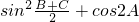的取值范围是[-，-]．分析：（1）欲求cosA根据条件，借助余弦定理即得
（2）利用降幂公式和二倍角公式化简成关于cosA的二次函数进行求解
点评：本题综合考查了余弦定理，二次函数的最值问题，通过换元法转化成二次函数进行求解．
练习册系列答案
相关题目