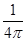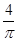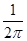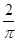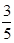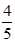题目内容
从装有 个红球和
个红球和 个黒球的口袋内任取
个黒球的口袋内任取 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
| A.至少有一个黒球与都是黒球 | B.至少有一个黑球与都是红球 |
C.至少有一个黒球与至少有 个红球 个红球 | D.恰有 个黒球与恰有 个黒球与恰有 个黒球 个黒球 |
D
解析试题分析:从装有 个红球和
个红球和 个黒球的口袋内任取
个黒球的口袋内任取 个球,所有的可能情况为:0红2黑,1红1黑,2红0黑。所以:
个球,所有的可能情况为:0红2黑,1红1黑,2红0黑。所以:
A.至少有一个黒球包括0红2黑和1红1黑,都是黒球为0红2黑,所以至少有一个黒球与都是黒球不互斥也不对立;
B.至少有一个黑球为0红2黑和1红1黑,都是红球 为2红0黑,所以至少有一个黑球与都是红球即对立又互斥;
C.至少有一个黒球为0红2黑和1红1黑,至少有 个红球为 1红1黑,2红0黑,所以至少有一个黒球与至少有
个红球为 1红1黑,2红0黑,所以至少有一个黒球与至少有 个红球不互斥也不对立;
个红球不互斥也不对立;
D.恰有 个黒球为1红1黑,恰有
个黒球为1红1黑,恰有 个黒球为0红2黑,所以恰有
个黒球为0红2黑,所以恰有 个黒球与恰有
个黒球与恰有 个黒球互斥但不对立。
个黒球互斥但不对立。
考点:互斥事件;对立事件。
点评:熟练掌握对立事件和互斥事件的概念。对立事件一定是互斥事件,但互斥事件不一定是对立事件。

练习册系列答案
相关题目
把一枚硬币连续抛掷两次,事件 “第一次出现正面”,事件
“第一次出现正面”,事件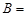 “第二次出现正面”,则
“第二次出现正面”,则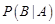 等于( )
等于( )
A.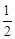 | B.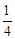 | C. | D. |
从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是( )
A.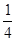 | B.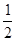 | C.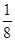 | D.无法确定 |
如果A,B是互斥事件,那么下列正确的是
A.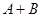 是必然事件 是必然事件 | B.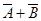 是必然事件 是必然事件 |
C.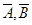 一定不互斥 一定不互斥 | D.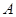 与 与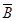 可能互斥也可能不互斥 可能互斥也可能不互斥 |
一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
| A.至多有一次中靶 | B.两次都中靶 |
| C.只有一次中靶 | D.两次都不中靶 |
.若h~B(2, p),且 ,则
,则 ( )
( )
A. | B. | C. | D. |

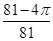
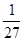
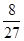
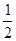 cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率是( )
cm的正方形孔,若你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率是( )