题目内容
【题目】已知函数![]() .
.
(Ⅰ)讨论函数![]() 的单调区间.
的单调区间.
(Ⅱ)当![]() 时,设
时,设![]() 的两个极值点
的两个极值点![]() ,
,![]()
![]() 恰为
恰为![]() 的零点,求
的零点,求![]() 的最小值.
的最小值.
【答案】(I)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,当
,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)求出函数![]() 的导数,讨论
的导数,讨论![]() 的取值,利用导数判断函数
的取值,利用导数判断函数![]() 的单调性与单调区间;(II)对函数
的单调性与单调区间;(II)对函数![]() 求导数,利用极值的定义得出
求导数,利用极值的定义得出![]() 时存在两正根
时存在两正根![]() 、
、![]() ;再利用判别式以及根与系数的关系,结合零点的定义,构造函数,利用导数即可求出函数
;再利用判别式以及根与系数的关系,结合零点的定义,构造函数,利用导数即可求出函数![]() 的最小值.
的最小值.
试题解析:(Ⅰ)![]() 函数
函数![]() ,
,![]() ,
,![]() ;
;
当![]() 时,由
时,由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
由![]() 解得
解得![]() ,即当
,即当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,故
,故![]() ,即
,即![]() 在
在![]() 上单调递增;
上单调递增;
![]() 当
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ; ...(5分)
; ...(5分)
(Ⅱ)![]() ,则
,则![]() ,
,
![]() 的两根
的两根![]() 、
、![]() 即为方程
即为方程![]() 的两根;
的两根;
又![]() ,
,
![]() ,
,![]() ,
,![]() ; ...(7分)
; ...(7分)
又![]() ,
,![]() 为
为![]() 的零点,
的零点,
![]() ,
,![]()
两式相减得![]() ,
,
得 ,
,
而![]() ,
,


 , ...(10分)
, ...(10分)
令![]() ,
,
由![]() 得
得![]() ,
,
因为![]() ,两边同时除以
,两边同时除以![]() ,得
,得![]() ,
,
![]() ,故
,故![]() ,解得
,解得![]() 或
或![]() ,
,![]() ; ...(12分)
; ...(12分)
设![]() ,
,
![]() ,则
,则![]() 在
在![]() 上是减函数,
上是减函数,
![]() .
.
即![]() 的最小值为
的最小值为![]() ...(14分)
...(14分)

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: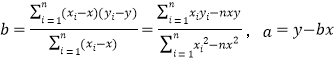 ,).
,).