Question

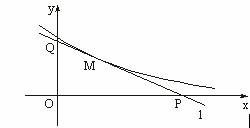
20.设曲线y=e^－x（x≥0）在点M（t,e^－t）处的切线l与x轴、y轴所围成的三角形面积为S（t）.

（Ⅰ）求切线l的方程;

（Ⅱ）求S（t）的最大值.

Answer 1

20.本题主要考查函数、导函数、不等式等基础知识,同时考查分析、推理和对基础知识的理解运用能力.

解：（Ⅰ）因为f′（x）=（e^－x）^t=－e^－x,

所以切线l的斜率为－e^－t.

故切线l的方程为y－e^－t=－e^－t（x－t）.即e^－tx+y－e^－t（t+1）=0.

（Ⅱ）令y=0得x=t+1,

又令x=0得y=e^－t（t+1）,

所以S（t）=（t+1）·e^－t（t+1）

=（t+1）²e^－t.

从而S′（t）= e^－t（1－t）（1+t）.

∵当t∈（0,1）时,S′（t）>0,

当t∈（1,+∞）时,S′（t）<0,

所以S（t）的最大值为S（1）=.