题目内容
已知数列{an}的前n项和Sn和通项an满足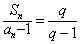 (q是常数且q>0,q≠1)。
(q是常数且q>0,q≠1)。
(1)求数列{an}的通项公式;
(2)当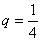 时,试证明
时,试证明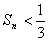 ;
;
(3)设函数f(x)=logqx,bn=f(a1)+f(a2)+…+f(an),是否存在正整数m,使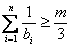 对
对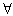 n∈N*都成立?若存在,求出m的值;若不存在,请说明理由。
n∈N*都成立?若存在,求出m的值;若不存在,请说明理由。
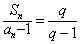 (q是常数且q>0,q≠1)。
(q是常数且q>0,q≠1)。(1)求数列{an}的通项公式;
(2)当
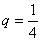 时,试证明
时,试证明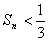 ;
;(3)设函数f(x)=logqx,bn=f(a1)+f(a2)+…+f(an),是否存在正整数m,使
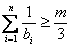 对
对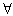 n∈N*都成立?若存在,求出m的值;若不存在,请说明理由。
n∈N*都成立?若存在,求出m的值;若不存在,请说明理由。解:(1)由题意,
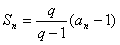 ,得
,得
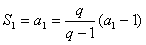
∴a1=q
当n≥2时,
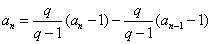
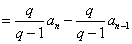
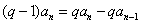
∴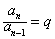
∴数列{an}是首项a1=q,公比为q的等比数列,故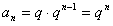 。
。
(2)由(1)知当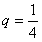 时,
时,
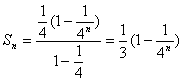 ,
,
∵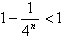
∴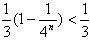
即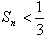 。
。
(3)∵f(x)=logqx
∴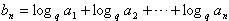

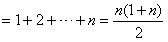
∴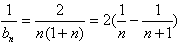
∴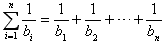
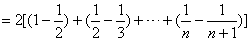
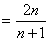
由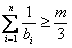 ,得
,得
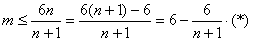
∵(*)对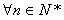 都成立,
都成立,
∴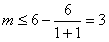
∵m是正整数,
∴m的值为1,2,3
∴使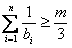 对
对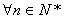 都成立的正整数m存在,其值为1,2,3。
都成立的正整数m存在,其值为1,2,3。
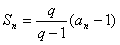 ,得
,得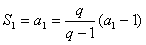
∴a1=q
当n≥2时,
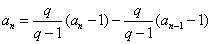
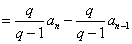
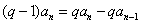
∴
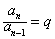
∴数列{an}是首项a1=q,公比为q的等比数列,故
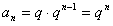 。
。(2)由(1)知当
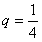 时,
时,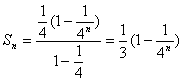 ,
,∵
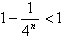
∴
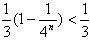
即
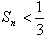 。
。(3)∵f(x)=logqx
∴
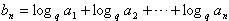

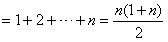
∴
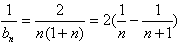
∴
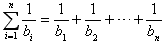
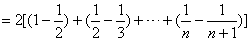
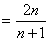
由
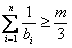 ,得
,得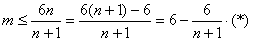
∵(*)对
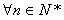 都成立,
都成立,∴
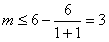
∵m是正整数,
∴m的值为1,2,3
∴使
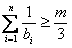 对
对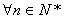 都成立的正整数m存在,其值为1,2,3。
都成立的正整数m存在,其值为1,2,3。
练习册系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |