题目内容
小明家订了一份报纸，寒假期间他收集了每天报纸送达时间的数据，并绘制成频率分布直方图，如图所示．
（1）根据图中的数据信息，写出众数
；
（2）小明的父亲上班离家的时间
在上午
之间，而送报人每天在时刻前后
半小时内把报纸送达（每个时间点送达的可能性相等）．
①求小明的父亲在上班离家前能收到报纸（称为事件
）的概率；
②求小明的父亲周一至周五在上班离家前能收到报纸的天数
的数学期望．
（1）
；（2）①
；②
.
解析试题分析：（1）在频率分布直方图中，众数是最高矩形的中点横坐标，即；（2）①基本事件总数有无限多个，故可以考虑几何概型．
可以看成平面中的点，试验的全部结果构成平面区域
，而事件A发生的前提是
，利用面积的比表示事件A发生的概率
；②小明的父亲周一至周五在上班离家前能收到报纸的天数相当于
次独立重复试验中，小明父亲收到报纸这个试验发生的次数，故随机变量服从二项分布∽
，则
.
试题解析：（1） 2分
①设报纸送达时间为
，小明父亲上班走的时间为，则小明父亲上班前能取到报纸
等价于
，如图可知，所求概率为
8分
②服从二项分布，故
（天） 12分
考点：1、众数；2、几何概型；3、二项分布.
练习册系列答案
相关题目
名.以下茎叶图记录了该小组同学在一次数学测试中的成绩(单位：分).已知男生数据的中位数为
，女生数据的平均数为
.
，
的值；
，
，
，
，
，
后得到如下图的频率分布直方图.
的车辆中任抽取3辆,求抽出的3辆车中车速在
的分布列及数学期望．
已知某地每单位面积菜地年平均使用氮肥量x(kg)与每单位面积蔬菜年平均产量y(t)之间的关系有如下数据：
| 年份 | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 | 1991 | 1992 |
| x(kg) | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
| y(t) | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
| | ||||||||
| 年份 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | |
| x(kg) | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
| y(t) | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 | |
(2)若线性相关，求蔬菜产量y与使用氮肥量x之间的回归直线方程，并估计每单位面积施肥150 kg时，每单位面积蔬菜的年平均产量．
(已知数据：
＝101，
≈10.113 3，
＝161 125，
＝1 628.55，
＝16 076.8) 某工厂生产
、
两种元件，其质量按测试指标划分为：大于或等于
为正品，小于为次品.现从一批产品中随机抽取这两种元件各
件进行检测，检测结果记录如下：
|  | | |  |  |
| B |  |  |  | |  |
、看不清，统计员只记得
，且、两种元件的检测数据的平均值相等，方差也相等.（1）求表格中
与的值；（2）从被检测的
件种元件中任取
件，求件都为正品的概率. 
，样本数据分组为
，
，
，
，
.
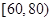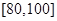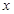的值；
分钟的新生，其中２人上学路上时间小于
分钟. 从这６人中任选２人，设这２人中上学路上时间小于
,求