题目内容

△ABC中，角A、B、C所对的边分别是a、b、c，tanA=，cosB=.

（1）求tanC的值；

（2）若△ABC最长的边的长为1，求最短的边长.

解：（1）因为B是三角形内角，

所以sinB===.所以tanB==.

所以tanC=tan(π-A-B)=-tan(A+B)===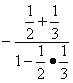-1.

（2）因为C是三角形内角，所以C=135°.又由已知，A、B都是锐角，且tanA＜tanB，

所以最长边c=1，最短边为b.

由正弦定理：,b==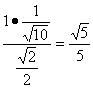,所以最短边为.

练习册系列答案
相关题目
（2012•丰台区一模）在△ABC中，角A，B，C所对的边分别为a，b，c，且asinB-bcosC=ccosB．
（Ⅰ）判断△ABC的形状；
（Ⅱ）若f(x)=
1
2
cos2x-
2
3
cosx+
1
2
，求f（A）的取值范围．
（2012•德州一模）已知函数f(x)=
3
sinxcosx-cos2x+
1
2
(x∈R)
（I）求函数f（x）的最小正周期及在区间[0，
5π
12
]上的值域；
（Ⅱ）在△ABC中，角A、B、C所对的边分别是a、b、c，又f(
A
2
+
π
3
)=
4
5
，b=2，面积S△ABC=3，求边长a的值．
（2012•卢湾区一模）在△ABC中，角A，B，C的对边分别为a，b，c，且a=2bcosC，b+c=3a．求sinA的值．
（2012•石景山区一模）在△ABC中，角A，B，C所对应的边分别为a，b，c，且（2a-c）cosB=bcosC．
（Ⅰ）求角B的大小；
（Ⅱ）若A=
π4
，a=2，求△ABC的面积．
在锐角△ABC中，角A、B、C所对的边长分别为a、b、c，向量
m
=(1，cosB)，
n
=(sinB，-
3
)，且
m
⊥
n
．
（1）求角B的大小；
（2）若△ABC面积为
3
3
2
，3ac=25-b2，求a，c的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网