题目内容
设角α=x(rad),且0＜x＜
,于是x,sinx,tanx都是实数,请你给x一个具体值,比较这三个实数的大小;然后想一想,你得到的大小关系是否对区间(0,
)上的任意x都成立?
解:(1)不妨取x=
,于是x=
,sinx=
,tanx=1,显然sinx＜x＜tanx.
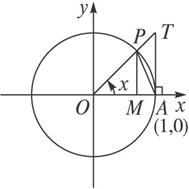
(2)如图,设角α的终边与单位圆交于点P,单位圆与x轴的正半轴的交点为A,过A点作圆的切线交OP的延长线于点T,连结AP,则sinx=MP,tanx=AT.
在△AOP中,
=x·OP=x.
由图易得S△POA＜S扇形POA＜S△AOT,
即
OA·MP＜
·OA＜
OA·AT,
所以MP＜
＜AT,
即sinx＜x＜tanx,
即对区间(0,
)上的任意x都成立.
练习册系列答案
津桥教育计算小状元系列答案
相关题目
,于是x,sinx,tanx都是实数,请你给x一个具体值,比较这三个实数的大小;然后想一想,你得到的大小关系是否对区间(0,
)上的任意x都成立?