题目内容

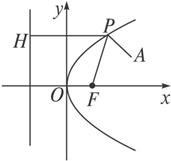
已知抛物线C的顶点在原点，焦点F在x轴的正半轴上.若抛物线上一动点P到A（2，）、F两点距离之和的最小值为4，求抛物线C的方程（其中A为抛物线内一点）.

解：如图，设抛物线方程为y2=2px(p＞0)，其准线为x=-,过P点作抛物线准线的垂线，垂足为H，由定义知|PH|=|PF|.当H、P、A三点共线时，|PA|+|PF|最小.所以|PF|+|PA|的最小值为+2=4,∴p=4.即y2=8x.

所以抛物线方程为y2=8x.

练习册系列答案
相关题目
精英家教网已知抛物线C的顶点在原点，焦点为F（0，1）．
（Ⅰ）求抛物线C的方程；
（Ⅱ）在抛物线C上是否存在点P，使得过点P的直线交C于另一点Q，满足PF⊥QF，且PQ与C在点P处的切线垂直？若存在，求出点P的坐标；若不存在，请说明理由．
（2010•温州一模）已知抛物线C的顶点在原点，焦点为F（0，1），且过点A（2，t），
（I）求t的值；
（II）若点P、Q是抛物线C上两动点，且直线AP与AQ的斜率互为相反数，试问直线PQ的斜率是否为定值，若是，求出这个值；若不是，请说明理由．
已知抛物线C的顶点在原点，焦点为F(
1
2
，0)．（1）求抛物线C的方程； （2）已知直线y=k(x+
1
2
) 与抛物线C交于A、B 两点，且|FA|=2|FB|，求k 的值； （3）设点P 是抛物线C上的动点，点R、N 在y 轴上，圆（x-1）2+y2=1 内切于△PRN，求△PRN 的面积最小值．
已知抛物线C的顶点在坐标原点，焦点F（1，0）．
（Ⅰ）求抛物线C的方程；
（Ⅱ）命题：“过抛物线C的焦点F作与x轴不垂直的任意直线l交抛物线于A、B两点，线段AB的垂直平分线交x轴于点M，则
|AB||FM|
为定值，且定值是2”．判断它是真命题还是假命题，并说明理；
（Ⅲ）试推广（Ⅱ）中的命题，写出关于抛物线的一般性命题（注，不必证明）．
已知抛物线C的顶点在坐标原点，以坐标轴为对称轴，且焦点F（2，0）．
（1）求抛物线C的标准方程；
（2）直线l过焦点F与抛物线C相交与M，N两点，且|MN|=16，求直线l的倾斜角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网