题目内容
函数y=4sinxcosx的最小正周期及最大值分别是
- A.2π，2
- B.π，2
- C.2π，1
- D.π，1
B
分析：将f（x）=sin2x-cos2x化成一角一函数的形式，然后确定最小正周期和最大值即可．
解答：y=4sinxcosx=2sin2x，最小正周期为π，最大值为2．
故选B．
点评：本题考查了三角函数的二倍正弦公式，以及三角函数的最小正周期及其最值，属于基础题型．
分析：将f（x）=sin2x-cos2x化成一角一函数的形式，然后确定最小正周期和最大值即可．
解答：y=4sinxcosx=2sin2x，最小正周期为π，最大值为2．
故选B．
点评：本题考查了三角函数的二倍正弦公式，以及三角函数的最小正周期及其最值，属于基础题型．
练习册系列答案
ABC考王全优卷系列答案
相关题目
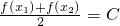成立（其中C为常数），则称函数y=f（x）在D上的约算术均值为C，则下列函数在其定义域上的算术均值可以为2的函数是