Question

（本小题满分12分）袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用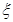表示取出的3个小球上的最大数字，求：

（Ⅰ）取出的3个小球上的数字互不相同的概率；

（Ⅱ）随机变量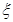的分布列和数学期望；

（Ⅲ）计分介于20分到40分之间的概率

 

Answer 1

【答案】

（Ⅰ）（Ⅱ）所以随机变量ξ的分布列为

ξ	2	3	4	5

（Ⅲ）

【解析】

试题分析：（Ⅰ）解法一：“一次取出的3个小球上的数字互不相同”的事件记为，

则

解法二：“一次取出的3个小球上的数字互不相同的事件记为A”，“一次取出的3个小球上有两个数字相同”的事件记为，则事件和事件是互斥事件，因为

所以 .                                        ……3分

（Ⅱ）由题意有可能的取值为：2，3，4，5

所以随机变量ξ的分布列为

ξ	2	3	4	5

因此的数学期望为

.                              ……9分

（Ⅲ）“一次取球所得计分介于20分到40分之间”的事件记为，则

                                                                      ……12分

考点：本小题主要考查离散型随机变量的分布列、期望等的求解，考查学生分析问题、解决问题的能力和运算求解能力.

点评：解决此类问题要注意判准事件的性质，根据事件的性质识别概率模型.