题目内容
【题目】已知椭圆C的左、右焦点坐标分别是![]() ,
,![]() ,离心率是
,离心率是![]() ,直线
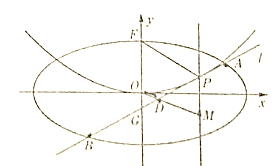
,直线![]() 与椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P.
与椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若圆P与x轴相切,求圆心P的坐标;
(Ⅲ)设Q(x,y)是圆P上的动点,当t变化时,求y的最大值.
【答案】(Ⅰ)![]() (Ⅱ)(0,
(Ⅱ)(0,![]() )(Ⅲ)2.
)(Ⅲ)2.
【解析】
解:(1)因为![]() =
=![]() ,且c=
,且c=![]() ,
,
所以a=![]() ,b=
,b=![]() =1.
=1.
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)由题意知P(0,t)(-1<t<1).
由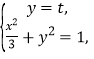
得x=±![]() .
.
所以圆P的半径为![]() .
.
当圆P与x轴相切时,|t|=![]() .
.
解得t=±![]() .
.
所以圆心P的坐标是(0,±![]() ).
).
(3)由(2)知,圆P的方程为x2+(y-t)2=3(1-t2).
因为点Q(x,y)在圆P上,
所以y=t±![]() ≤t+
≤t+![]() .
.
设t=cos θ,θ∈(0,π),
则t+![]() =cos θ+
=cos θ+![]() sin θ=2sin(θ+
sin θ=2sin(θ+![]() ).
).
当θ=![]() ,即t=
,即t=![]() ,且x=0时,y取最大值2.
,且x=0时,y取最大值2.

练习册系列答案
相关题目
【题目】据长期统计分析,某货物每天的需求量![]() 在17与26之间,日需求量
在17与26之间,日需求量![]() (件)的频率
(件)的频率![]() 分布如下表所示:
分布如下表所示:
需求量 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
频率 | 0.12 | 0.18 | 0.23 | 0.13 | 0.10 | 0.08 | 0.05 | 0.04 | 0.04 | 0.03 |
已知其成本为每件5元,售价为每件10元.若供大于求,则每件需降价处理,处理价每件2元.假设每天的进货量必需固定.
(1)设每天的进货量为![]() ,视日需求量
,视日需求量![]() 的频率为概率
的频率为概率![]() ,求在每天进货量为
,求在每天进货量为![]() 的条件下,日销售量
的条件下,日销售量![]() 的期望值
的期望值![]() (用
(用![]() 表示);
表示);
(2)在(1)的条件下,写出![]() 和
和![]() 的关系式,并判断
的关系式,并判断![]() 为何值时,日利润的均值最大?
为何值时,日利润的均值最大?