题目内容
已知函数f(x)=x2+
(x≠0,常数a∈R).
(1)当a=1时,解不等式f(x)>
(2)讨论函数f(x)的奇偶性,并说明理由.
| a |
| x |
(1)当a=1时,解不等式f(x)>
| 2 |
| x |
(2)讨论函数f(x)的奇偶性,并说明理由.
考点:其他不等式的解法,函数奇偶性的判断
专题:不等式的解法及应用
分析:(1)当a=1时,原不等式可化为
>0,解之即可;
(2)分a=0与a≠0讨论,利用奇偶函数的定义判断即可.
(1-x)[(x+
| ||||
| x |
(2)分a=0与a≠0讨论,利用奇偶函数的定义判断即可.
解答:
解:(1)当a=1时,x2+
>
,即x2>
,即
>0,
解得:x>1或x<0;…(6分)
(2)当a=0时,f(x)=x2,
对任意x∈(-∞,0)∪(0,+∞),
f(-x)=(-x)2=x2=f(x),∴f(x)为偶函数.
当a≠0时,f(x)=x2+
(a≠0,x≠0),
取x=±1,得 f(-1)+f(1)=2≠0,f(-1)-f(1)=-2a≠0,
∴f(-1)≠-f(1),f(-1)≠f(1),
∴函数f(x)既不是奇函数,也不是偶函数. ….(13分)
| 1 |
| x |
| 2 |
| x |
| 1 |
| x |
(1-x)[(x+
| ||||
| x |
解得:x>1或x<0;…(6分)
(2)当a=0时,f(x)=x2,
对任意x∈(-∞,0)∪(0,+∞),
f(-x)=(-x)2=x2=f(x),∴f(x)为偶函数.
当a≠0时,f(x)=x2+
| a |
| x |
取x=±1,得 f(-1)+f(1)=2≠0,f(-1)-f(1)=-2a≠0,
∴f(-1)≠-f(1),f(-1)≠f(1),
∴函数f(x)既不是奇函数,也不是偶函数. ….(13分)
点评:本题考查分式不等式的解法,着重考查函数奇偶性的判定,考查转化思想与运算求解能力,属于中档题.

练习册系列答案
相关题目
已知
和
是两个单位向量,夹角为
,则下面向量中与2
-
垂直的是( )
| e1 |
| e2 |
| π |
| 3 |
| e2 |
| e1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
解下列不等式:
(1)|4x-3|<21;
(2)|
+2|≥
;
(3)
>
;
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
(1)|4x-3|<21;
(2)|
| x-1 |
| 2 |
| 3 |
| 4 |
(3)
| |3x-1|-1 |
| 2 |
| |1-3x|+1 |
| 3 |
(4)|x+3|>x+3;
(5)|3x-4|>2x-1;
(6)|3x-4|≤x-1.
设2b是1-a和1+a的等比中项,则a+4b的最大值为( )
| A、1 | ||||
| B、3 | ||||
C、
| ||||
D、
|
 已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为
已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,圆M与y轴相切,过原点O作倾斜角为
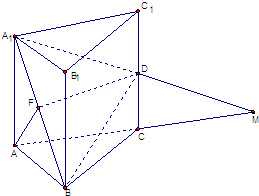 已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),
已知正三棱柱A1B1C1-ABC中,AA1=AB=a,D是CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M(如图),