题目内容
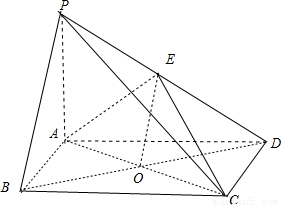
如图,四棱锥P-ABCD的底面是菱形,PA⊥底面ABCD,E是PD的中点;(Ⅰ)求证:PB∥平面ACE;
(Ⅱ)求证:BD⊥PC.

【答案】分析:(Ⅰ)取AC与BD的交点为O,连EO,利用EO为三角形PBD的中位线和线面平行的判定定理即可证得PB∥平面ACE;
(Ⅱ)易证BD⊥平面PAC,利用直线与平面垂直的性质即可证得BD⊥PC.
解答:证明:(Ⅰ)∵底面ABCD是菱形,取AC与BD的交点为O,又E是PD的中点,连EO,
则EO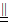
 PB,
PB,
又EO?平面ACE,PB?平面ACE,
∴PB∥平面ACE;
(Ⅱ)∵PA⊥底面ABCD,BD?底面ABCD,
∴PA⊥BD;①
又底面ABCD是菱形,
∴AC⊥BD;②
PA∩AC=A,
∴BD⊥平面PAC,PC?平面PAC,
∴BD⊥PC.
点评:本题考查直线与平面平行的判定,考查直线与平面垂直的性质,属于中档题.
(Ⅱ)易证BD⊥平面PAC,利用直线与平面垂直的性质即可证得BD⊥PC.
解答:证明:(Ⅰ)∵底面ABCD是菱形,取AC与BD的交点为O,又E是PD的中点,连EO,

则EO
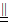
 PB,
PB,又EO?平面ACE,PB?平面ACE,
∴PB∥平面ACE;
(Ⅱ)∵PA⊥底面ABCD,BD?底面ABCD,
∴PA⊥BD;①
又底面ABCD是菱形,
∴AC⊥BD;②
PA∩AC=A,
∴BD⊥平面PAC,PC?平面PAC,
∴BD⊥PC.
点评:本题考查直线与平面平行的判定,考查直线与平面垂直的性质,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=