题目内容
(在给出的二个题中,任选一题作答.若多选做,则按所做的第A题给分)
(A)(坐标系与参数方程)在极坐标系中,直线 的位置关系是________.
的位置关系是________.
(B)(不等式选讲)已知对于任意非零实数m,不等式 恒成立,则实数x的取值范围是________.
恒成立,则实数x的取值范围是________.
相离 (-∞,-1]∪(0,2]
分析:(A)先将直线l的发送坐标方程化成直线的普通方程,利用极坐标转化成直角坐标的转换公式求出圆的直角坐标方程;欲判断直线l和圆C的位置关系,只需求圆心到直线的距离与半径进行比较即可,根据点到线的距离公式求出圆心到直线的距离然后与半径比较.
(B)首先分析题目已知不等式 恒成立,可变形为
恒成立,可变形为  恒成立,又因为根据绝对值不等式可得到右边大于等于1.即可得到
恒成立,又因为根据绝对值不等式可得到右边大于等于1.即可得到 ≤1,利用分式不等式的解法即可求得x的取值范围.
≤1,利用分式不等式的解法即可求得x的取值范围.
解答:(A)直线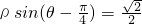 ,即ρsinθ-ρcosθ-1=0,
,即ρsinθ-ρcosθ-1=0,
得直线l的普通方程为x-y+1=0,
ρ=2cosθ,两边同乘以ρ得ρ2=2ρcosθ,
得⊙C的直角坐标方程为(x-1)2+y2=1;
圆心C到直线l的距离 ,
,
所以直线l和⊙C相离.
故答案为:相离.
(B)解:已知对于任意非零实数m,
已知不等式 恒成立,
恒成立,
可变形为 恒成立,
恒成立,
因为:
所以只需 ≤1?
≤1?
得x的取值范围为(-∞,-1]∪(0,2],
故答案为(-∞,-1]∪(0,2].
点评:(A)本题主要考查了简单曲线的极坐标方程,以及直线的参数方程和直线与圆的位置关系的判定,属于基础题.
(B)此题主要考查绝对值不等式的应用问题,有一定的灵活性,题中应用到分式不等式的解法,属于基础题目.
分析:(A)先将直线l的发送坐标方程化成直线的普通方程,利用极坐标转化成直角坐标的转换公式求出圆的直角坐标方程;欲判断直线l和圆C的位置关系,只需求圆心到直线的距离与半径进行比较即可,根据点到线的距离公式求出圆心到直线的距离然后与半径比较.
(B)首先分析题目已知不等式
 恒成立,可变形为
恒成立,可变形为  恒成立,又因为根据绝对值不等式可得到右边大于等于1.即可得到
恒成立,又因为根据绝对值不等式可得到右边大于等于1.即可得到 ≤1,利用分式不等式的解法即可求得x的取值范围.
≤1,利用分式不等式的解法即可求得x的取值范围.解答:(A)直线
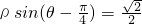 ,即ρsinθ-ρcosθ-1=0,
,即ρsinθ-ρcosθ-1=0,得直线l的普通方程为x-y+1=0,
ρ=2cosθ,两边同乘以ρ得ρ2=2ρcosθ,
得⊙C的直角坐标方程为(x-1)2+y2=1;
圆心C到直线l的距离
 ,
,所以直线l和⊙C相离.
故答案为:相离.
(B)解:已知对于任意非零实数m,
已知不等式
 恒成立,
恒成立,可变形为
 恒成立,
恒成立,因为:

所以只需
 ≤1?
≤1?
得x的取值范围为(-∞,-1]∪(0,2],
故答案为(-∞,-1]∪(0,2].
点评:(A)本题主要考查了简单曲线的极坐标方程,以及直线的参数方程和直线与圆的位置关系的判定,属于基础题.
(B)此题主要考查绝对值不等式的应用问题,有一定的灵活性,题中应用到分式不等式的解法,属于基础题目.

练习册系列答案
相关题目
 与圆
与圆 的位置关系是 。
的位置关系是 。 ,不等式
,不等式 恒成立,则实数
恒成立,则实数 的取值范围是 。
的取值范围是 。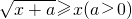 的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为________.
的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为________. 的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为______.
的解集为{x|m≤x≤n},且|m-n|=2a,则a的取值集合为______.