题目内容
定义域为R的函数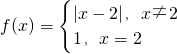
，若关于x的方程f2（x）+bf（x）+c=0恰有5个不同的实数解x1，x2，x3，x4，x5，则f（x1+x2+x3+x4+x5）等于
- A.0
- B.2
- C.8
- D.10
C
分析：先根据一元二次方程根的情况可判断f（2）一定是一个解，再假设f（x）的一解为A可得到x1+x2=4，同理可得到x3+x4=4，进而可得到x1+x2+x3+x4+x5=10，
然后代入函数f（x）的解析式即可得到最后答案．
解答：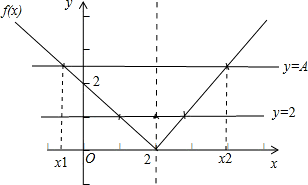
解：对于f2（x）+bf（x）+c=0来说，f（x）最多只有2解，又当x不等于2时，x最多四个解，不满足题中的条件．
而题目要求5解，即可推断f（2）必为方程的一解．
假设f（x）的一个解为A，得f（x）=|x-2|=A，推出 x1=2+A，x2=2-A，∴x1+x2=4．
同理可得 x3+x4=4，∴x1+x2+x3+x4+x5=4+4+2=10，
∴f（x1+x2+x3+x4+x5）=f（10）=|10-2|=8，
故选C．
点评：本题主要考查一元二次方程根的情况，和含有绝对值的函数的解法，考查基础知识的综合运用能力，体现了转化和数形结合的数学思想，属于中档题．
分析：先根据一元二次方程根的情况可判断f（2）一定是一个解，再假设f（x）的一解为A可得到x1+x2=4，同理可得到x3+x4=4，进而可得到x1+x2+x3+x4+x5=10，
然后代入函数f（x）的解析式即可得到最后答案．
解答：
解：对于f2（x）+bf（x）+c=0来说，f（x）最多只有2解，又当x不等于2时，x最多四个解，不满足题中的条件．而题目要求5解，即可推断f（2）必为方程的一解．
假设f（x）的一个解为A，得f（x）=|x-2|=A，推出 x1=2+A，x2=2-A，∴x1+x2=4．
同理可得 x3+x4=4，∴x1+x2+x3+x4+x5=4+4+2=10，
∴f（x1+x2+x3+x4+x5）=f（10）=|10-2|=8，
故选C．
点评：本题主要考查一元二次方程根的情况，和含有绝对值的函数的解法，考查基础知识的综合运用能力，体现了转化和数形结合的数学思想，属于中档题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
，若关于x的方程f2（x）+bf（x）+c=0有3个不同的整数解x1，x2，x3，则x12+x22+x32等于 ．
，若关于x的方程f2（x）+bf（x）+c=0有3个不同的整数解x1，x2，x3，则x12+x22+x32等于 ．
，若关于
的方程
有3个不同的实根，则关于x的不等式
的解集为( )
D． (c,1)
，若关于
的方程
有3个不同的实根
，则
等于
C． 13 D． 