题目内容
若函数f（x）=4x3-ax+3的单调递减区间是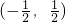
，则实数a的值为________．
3
分析：求出导函数，令导函数小于0的解集为单调递减区间；得到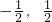
是导函数的两个零点，代入求出a．
解答：f′（x）=12x2-a
∵f（x）=4x3-ax+3的单调递减区间是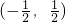
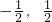∴是12x2-a=0的两个根
所以a=3
故答案为3
点评：本题考查利用导函数求函数的单调区间：导函数大于0对应的x的范围是函数的递增区间；导函数小于0对应的x的范围是函数的递减区间．
分析：求出导函数，令导函数小于0的解集为单调递减区间；得到
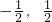是导函数的两个零点，代入求出a．解答：f′（x）=12x2-a
∵f（x）=4x3-ax+3的单调递减区间是
∴
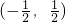
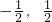是12x2-a=0的两个根所以a=3
故答案为3
点评：本题考查利用导函数求函数的单调区间：导函数大于0对应的x的范围是函数的递增区间；导函数小于0对应的x的范围是函数的递减区间．
练习册系列答案
相关题目
若函数f（x）=
，则f（log43）=（ ）
|
A、
| ||
B、
| ||
| C、3 | ||
| D、4 |