题目内容
(2013•福建)若2x+2y=1,则x+y的取值范围是( )
分析:根据指数式的运算性质结合基本不等式可把条件转化为关于x+y的不等关系式,进而可求出x+y的取值范围.
解答:解:∵1=2x+2y≥2•(2x2y)
,
变形为2x+y≤
,即x+y≤-2,当且仅当x=y时取等号.
则x+y的取值范围是(-∞,-2].
故选D.
| 1 |
| 2 |
变形为2x+y≤
| 1 |
| 4 |
则x+y的取值范围是(-∞,-2].
故选D.
点评:利用基本不等式,构造关于某个变量的不等式,解此不等式便可求出该变量的取值范围,再验证等号是否成立,便可确定该变量的最值,这是解决最值问题或范围问题的常用方法,应熟练掌握.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
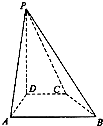 (2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.
(2013•福建)如图,在四棱柱P-ABCD中,PD⊥平面ABCD,AB∥DC,AB⊥AD,BC=5,DC=3,AD=4,∠PAD=60°.