题目内容
已知函数f（x）=-x2+3x+1x∈[m，m+1]．
（1）求f（x）的最大值g（m）；
（2）当m≥1，求g（m）的最大值．
解：（1）当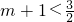
，即
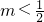时，
g（m）=f（m+1）=-m2+m+3；
当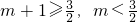
时，
即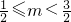
时，g（m）=
；
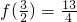当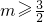
时，g（m）=f（m）=-m2+3m+1．
所以，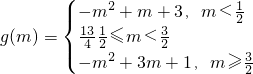
（2）当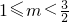
时，g（m）=
，
当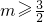时，g（m）=-m2+3m+1的最大值为，
综上，当m≥1，求g（m）的最大值为．
分析：（1）首先进行配方，然后利用对称轴与区间的位置关系进行合理地分类，若在区间内单调，则在端点处取得最值；若顶点在区间内，则在顶点处取得最值，结果为一分段函数的形式，
（2）分段函数求最值就是求出各段函数的最值后比较大小就可求出．
点评：本题考查了定函数在动区间上的最值问题，以及分段函数求最值．
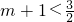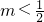，即时，g（m）=f（m+1）=-m2+m+3；
当
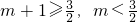时，即
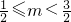时，g（m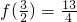）=；当
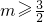时，g（m）=f（m）=-m2+3m+1．所以，
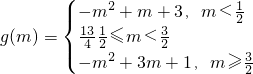
（2）当
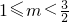时，g（m）=，当
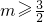时，g（m）=-m2+3m+1的最大值为，综上，当m≥1，求g（m）的最大值为
．分析：（1）首先进行配方，然后利用对称轴与区间的位置关系进行合理地分类，若在区间内单调，则在端点处取得最值；若顶点在区间内，则在顶点处取得最值，结果为一分段函数的形式，
（2）分段函数求最值就是求出各段函数的最值后比较大小就可求出．
点评：本题考查了定函数在动区间上的最值问题，以及分段函数求最值．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|