Question

已知二次函数f(x)=ax²+bx满足f(2)=0且方程f(x)=0有等根.

(1)求f(x)的解析式；

(2)问是否存在实数m、n(m＜n)，使f(x)的定义域为［m，n］，值域为［2m，2n］?如存在，求出m、n的值；如不存在，请说明理由.

Answer 1

解:(1)依题意，方程ax²+(b－1)x=0有等根，

∴(b－1)²=0,即b=1.

又f(2)=0，∴4a+2b=0.∴a=－.

∴f(x)=－x²+x.

(2)∵f(x)=－ (x－1)²+≤,

∴2n≤，即n≤.

∵f(x)=－(x－1)²+的对称轴为x=1,

∴当n≤时，f(x)在［m，n］上为增函数.

设m、n存在，则即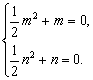

又m＜n≤，∴

即存在实数m=－2，n=0，使f(x)的定义域为［－2，0］，值域为［－4，0］.

点评:二次函数问题是函数中的重要题型，本题先用待定系数法确定解析式，然后再用m、n把定义域、值域联系起来，考查二次函数性质.