题目内容
已知函数f(x)= ln(1-x)(a∈R),e为自然对数的底数.
ln(1-x)(a∈R),e为自然对数的底数.
(1)求f(x)在区间[1-e2,1-e]上的最值;
(2)若n≥2(n∈N*),试比较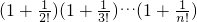 与e的大小,并证明你的结论.
与e的大小,并证明你的结论.
解:(1) ,设h(x)=x+ln(1-x),x∈R,
,设h(x)=x+ln(1-x),x∈R,
则 ,即h(x)在(-∞,0]上递增,故h(x)<h(0)=a,
,即h(x)在(-∞,0]上递增,故h(x)<h(0)=a,
即对x∈[1-e2,1-e],有h(x)<a.
①当a>0,有f(x)>0,f(x)在[1-e2,1-e]上递增
故 ,
, .
.
②当a<0,有f(x)<0,f(x)在[1-e2,1-e]上递减,
故 .
.
③当a=0,有f(x)=0,f(x)min=f(x)max=0.
(2)若n≥2(n∈N*),猜想: .
.
证明如下:据(1)知当x≤0时恒有h(x)≤0,即ln(1-x)≤-x
故


故 .
.
分析:(1)对函数f(x)求导,利用导函数,当导函数为0时,求出函数的增减区间,即可求最值;
(2)对a分情况讨论,通过放缩不等式,使不等式变成已有的简单式子进行证明.
点评:本题主要考查了利用导数求最值以及不等式的证明,不等式的合理放缩是解题的关键.
 ,设h(x)=x+ln(1-x),x∈R,
,设h(x)=x+ln(1-x),x∈R,则
 ,即h(x)在(-∞,0]上递增,故h(x)<h(0)=a,
,即h(x)在(-∞,0]上递增,故h(x)<h(0)=a,即对x∈[1-e2,1-e],有h(x)<a.
①当a>0,有f(x)>0,f(x)在[1-e2,1-e]上递增
故
 ,
, .
.②当a<0,有f(x)<0,f(x)在[1-e2,1-e]上递减,
故
 .
.③当a=0,有f(x)=0,f(x)min=f(x)max=0.
(2)若n≥2(n∈N*),猜想:
 .
.证明如下:据(1)知当x≤0时恒有h(x)≤0,即ln(1-x)≤-x
故



故
 .
.分析:(1)对函数f(x)求导,利用导函数,当导函数为0时,求出函数的增减区间,即可求最值;
(2)对a分情况讨论,通过放缩不等式,使不等式变成已有的简单式子进行证明.
点评:本题主要考查了利用导数求最值以及不等式的证明,不等式的合理放缩是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目