题目内容
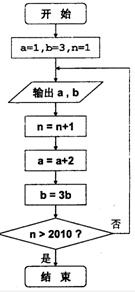 根据如图所示的程序框图,将输出的a,b值依次分别记为a1,a2,…,an,b1,b2,…,bn,其中n∈N*,n≤2010.
根据如图所示的程序框图,将输出的a,b值依次分别记为a1,a2,…,an,b1,b2,…,bn,其中n∈N*,n≤2010.(I)分别求数列{an}和{bn}的通项公式;
(II)令cn=anbn,求数列{cn}的前n项和Tn.
分析:(I)根据框图可知an+1=an+2整理得an+1-an=2,根据等差数列的定义判断出{an}为等差数列,进而根据等差数列的通项公式求得an,根据bn+1=3bn,整理得
=3判断出{bn}为等比数列,根据首项和公比求得{bn}的通项公式.
(II)根据(1)中求得的an和bn,求得cn,进而利用错位相减法求得答案.
| bn+1 |
| bn |
(II)根据(1)中求得的an和bn,求得cn,进而利用错位相减法求得答案.
解答:解:(I)依框图得,an+1=an+2,a1=1,
即an+1-an=2,∴数列{an}是首项为1,公差为2的等差数列
∴an=1+(n-1)×2=2n-1
又bn+1=3bn,b1=3,
即
=3,∴数列{bn}是首项为3,公比为3的等比数列
∴bn=3×3n-1=3n
(II)由(I)得cn=anbn=(2n-1)•3n
∵数列{cn}的前n和为Tn∴Tn=c1+c2+c3++cn-1+cnTn=1×31+3×32+5×33++(2n-3)×3n-1+(2n-1)×3n①
∴3Tn=1×32+3×33+5×34++(2n-3)×3n+(2n-1)×3n+1②
将①-②得:-2Tn=3+2×32+2×33+2×34++2×3n-(2n-1)×3n+1=-3+2(3+32+33+34++3n)-(2n-1)×3n+1
=-3+2×
-(2n-1)×3n+1=-2(n-1)×3n+1-6
Tn=(n-1)×3n+1+3
即an+1-an=2,∴数列{an}是首项为1,公差为2的等差数列
∴an=1+(n-1)×2=2n-1
又bn+1=3bn,b1=3,
即
| bn+1 |
| bn |
∴bn=3×3n-1=3n
(II)由(I)得cn=anbn=(2n-1)•3n
∵数列{cn}的前n和为Tn∴Tn=c1+c2+c3++cn-1+cnTn=1×31+3×32+5×33++(2n-3)×3n-1+(2n-1)×3n①
∴3Tn=1×32+3×33+5×34++(2n-3)×3n+(2n-1)×3n+1②
将①-②得:-2Tn=3+2×32+2×33+2×34++2×3n-(2n-1)×3n+1=-3+2(3+32+33+34++3n)-(2n-1)×3n+1
=-3+2×
| 3(3n-1) |
| 3-1 |
Tn=(n-1)×3n+1+3
点评:本题主要考查了等差数列和等比数列的通项公式,及数列求和问题.由等差数列和等比数列构成的数列常可用错位相减法求和.

练习册系列答案
相关题目
 25、按如图所示的程序框图操作:
25、按如图所示的程序框图操作: 按如图所示的程序框图操作:
按如图所示的程序框图操作: 按如图所示的程序框图操作:
按如图所示的程序框图操作: 按如图所示的程序框图操作:
按如图所示的程序框图操作: