题目内容
6．三视图如图所示的几何体的全面积是7+$\sqrt{2}$．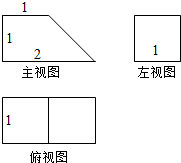
分析 根据几何体的三视图，得出该几何体是底面为直角梯形的直四棱柱，结合图中数据求出它的全面积．
解答 解：根据几何体的三视图，得；
该几何体是底面为直角梯形的直四棱柱，
且直角梯形的上底为1，下底为2，高为1，
四棱柱的棱长为1；
所以该四棱柱的全面积为
2×$\frac{1}{2}$×（1+2）×1+（1×1+1×1+2×1+1×$\sqrt{{1}^{2}{+1}^{2}}$）=7+$\sqrt{2}$．
故答案为：7+$\sqrt{2}$．
点评 本题考查了利用空间几何体的三视图求全面积的应用问题，是基础题目．
练习册系列答案
相关题目
16．已知i为虚数单位，复数$\frac{1-i}{2i+1}$的共扼复数在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |